Алгоритм сжатия Хаффмана

В преддверии старта курса «Алгоритмы для разработчиков» подготовили для вас перевод еще одного полезного материала.

Кодирование Хаффмана – это алгоритм сжатия данных, который формулирует основную идею сжатия файлов. В этой статье мы будем говорить о кодировании фиксированной и переменной длины, уникально декодируемых кодах, префиксных правилах и построении дерева Хаффмана.

Мы знаем, что каждый символ хранится в виде последовательности из 0 и 1 и занимает 8 бит. Это называется кодированием фиксированной длины, поскольку каждый символ использует одинаковое фиксированное количество битов для хранения.

Допустим, дан текст. Каким образом мы можем сократить количество места, требуемого для хранения одного символа?

Основная идея заключается в кодировании переменной длины. Мы можем использовать тот факт, что некоторые символы в тексте встречаются чаще, чем другие (см. здесь), чтобы разработать алгоритм, который будет представлять ту же последовательность символов меньшим количеством битов. При кодировании переменной длины мы присваиваем символам переменное количество битов в зависимости от частоты их появления в данном тексте. В конечном итоге некоторые символы могут занимать всего 1 бит, а другие 2 бита, 3 или больше. Проблема с кодированием переменной длины заключается лишь в последующем декодировании последовательности.

Как, зная последовательность битов, декодировать ее однозначно?

Рассмотрим строку «aabacdab». В ней 8 символов, и при кодировании фиксированной длины для ее хранения понадобится 64 бита. Заметим, что частота символов «a», «b», «c» и «d» равняется 4, 2, 1, 1 соответственно. Давайте попробуем представить «aabacdab» меньшим количеством битов, используя тот факт, что «a» встречается чаще, чем «b», а «b» встречается чаще, чем «c» и «d». Начнем мы с того, что закодируем «a» с помощью одного бита, равного 0, «b» мы присвоим двухбитный код 11, а с помощью трех битов 100 и 011 закодируем «c» и «d».

В итоге у нас получится:

a
0

b
11

c
100

d
011

Таким образом строку «aabacdab» мы закодируем как 00110100011011 (0|0|11|0|100|011|0|11), используя коды, представленные выше. Однако основная проблема будет в декодировании. Когда мы попробуем декодировать строку 00110100011011, у нас получится неоднозначный результат, поскольку ее можно представить как:

0|011|0|100|011|0|11    adacdab
0|0|11|0|100|0|11|011   aabacabd
0|011|0|100|0|11|0|11   adacabab 

…
и т.д.

Чтобы избежать этой неоднозначности, мы должны гарантировать, что наше кодирование удовлетворяет такому понятию, как префиксное правило, которое в свою очередь подразумевает, что коды можно декодировать всего одним уникальным способом. Префиксное правило гарантирует, что ни один код не будет префиксом другого. Под кодом мы подразумеваем биты, используемые для представления конкретного символа. В приведенном выше примере 0 – это префикс 011, что нарушает префиксное правило. Итак, если наши коды удовлетворяют префиксному правилу, то можно однозначно провести декодирование (и наоборот).

Давайте пересмотрим пример выше. На этот раз мы назначим для символов «a», «b», «c» и «d» коды, удовлетворяющие префиксному правилу.

a
0

b
10

c
110

d
111

С использованием такого кодирования, строка «aabacdab» будет закодирована как 00100100011010 (0|0|10|0|100|011|0|10). А вот 00100100011010 мы уже сможем однозначно декодировать и вернуться к нашей исходной строке «aabacdab».

Кодирование Хаффмана

Теперь, когда мы разобрались с кодированием переменной длины и префиксным правилом, давайте поговорим о кодировании Хаффмана.

Метод основывается на создании бинарных деревьев. В нем узел может быть либо конечным, либо внутренним. Изначально все узлы считаются листьями (конечными), которые представляют сам символ и его вес (то есть частоту появления). Внутренние узлы содержат вес символа и ссылаются на два узла-наследника. По общему соглашению, бит «0» представляет следование по левой ветви, а «1» — по правой. В полном дереве N листьев и N-1 внутренних узлов. Рекомендуется, чтобы при построении дерева Хаффмана отбрасывались неиспользуемые символы для получения кодов оптимальной длины.

Мы будем использовать очередь с приоритетами для построения дерева Хаффмана, где узлу с наименьшей частотой будет присвоен высший приоритет. Ниже описаны шаги построения:

1. Создайте узел-лист для каждого символа и добавьте их в очередь с приоритетами.
2. Пока в очереди больше одного листа делаем следующее:
   • Удалите два узла с наивысшим приоритетом (с самой низкой частотой) из очереди;
   • Создайте новый внутренний узел, где эти два узла будут наследниками, а частота появления будет равна сумме частот этих двух узлов.
   • Добавьте новый узел в очередь приоритетов.
3. Единственный оставшийся узел будет корневым, на этом построение дерева закончится.

Представим, что у нас есть некоторый текст, который состоит только из символов «a», «b», «c», «d» и «e», а частоты их появления равны 15, 7, 6, 6 и 5 соответственно. Ниже приведены иллюстрации, которые отражают шаги алгоритма.

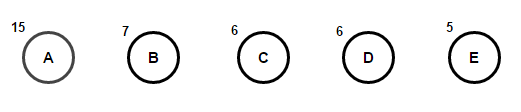
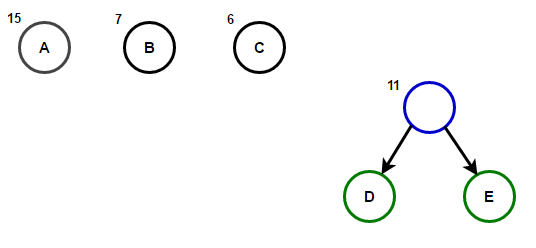
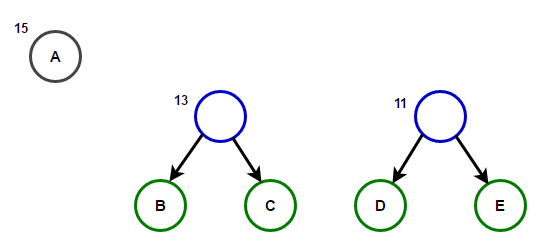
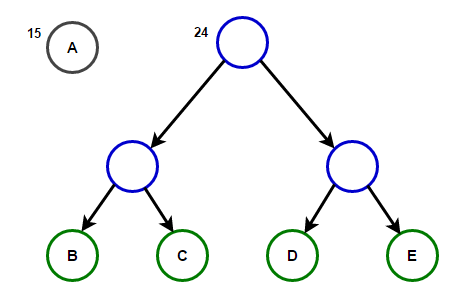
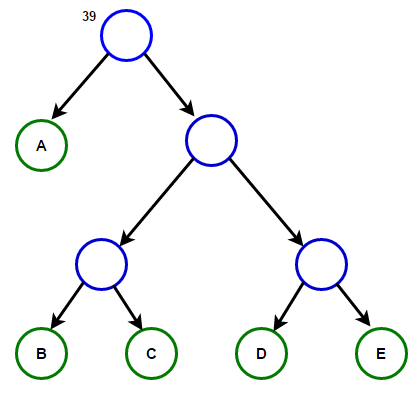
Путь от корня до любого конечного узла будет хранить оптимальный префиксный код (также известный, как код Хаффмана), соответствующий символу, связанному с этим конечным узлом.

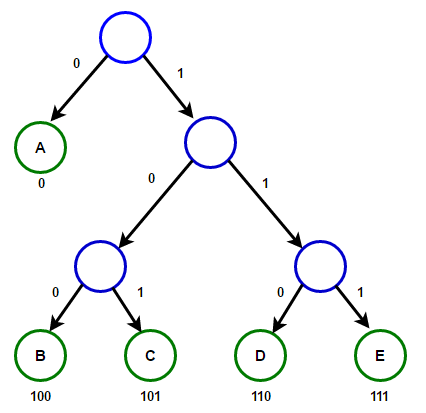
Дерево Хаффмана

Ниже вы найдете реализацию алгоритма сжатия Хаффмана на языках C++ и Java:

#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;

// A Tree node
struct Node
{
	char ch;
	int freq;
	Node *left, *right;
};

// Function to allocate a new tree node
Node* getNode(char ch, int freq, Node* left, Node* right)
{
	Node* node = new Node();

	node->ch = ch;
	node->freq = freq;
	node->left = left;
	node->right = right;

	return node;
}

// Comparison object to be used to order the heap
struct comp
{
	bool operator()(Node* l, Node* r)
	{
		// highest priority item has lowest frequency
		return l->freq > r->freq;
	}
};

// traverse the Huffman Tree and store Huffman Codes
// in a map.
void encode(Node* root, string str,
			unordered_map<char, string> &huffmanCode)
{
	if (root == nullptr)
		return;

	// found a leaf node
	if (!root->left && !root->right) {
		huffmanCode[root->ch] = str;
	}

	encode(root->left, str + "0", huffmanCode);
	encode(root->right, str + "1", huffmanCode);
}

// traverse the Huffman Tree and decode the encoded string
void decode(Node* root, int &index, string str)
{
	if (root == nullptr) {
		return;
	}

	// found a leaf node
	if (!root->left && !root->right)
	{
		cout << root->ch;
		return;
	}

	index++;

	if (str[index] =='0')
		decode(root->left, index, str);
	else
		decode(root->right, index, str);
}

// Builds Huffman Tree and decode given input text
void buildHuffmanTree(string text)
{
	// count frequency of appearance of each character
	// and store it in a map
	unordered_map<char, int> freq;
	for (char ch: text) {
		freq[ch]++;
	}

	// Create a priority queue to store live nodes of
	// Huffman tree;
	priority_queue<Node*, vector<Node*>, comp> pq;

	// Create a leaf node for each character and add it
	// to the priority queue.
	for (auto pair: freq) {
		pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
	}

	// do till there is more than one node in the queue
	while (pq.size() != 1)
	{
		// Remove the two nodes of highest priority
		// (lowest frequency) from the queue
		Node *left = pq.top(); pq.pop();
		Node *right = pq.top();	pq.pop();

		// Create a new internal node with these two nodes
		// as children and with frequency equal to the sum
		// of the two nodes' frequencies. Add the new node
		// to the priority queue.
		int sum = left->freq + right->freq;
		pq.push(getNode('', sum, left, right));
	}

	// root stores pointer to root of Huffman Tree
	Node* root = pq.top();

	// traverse the Huffman Tree and store Huffman Codes
	// in a map. Also prints them
	unordered_map<char, string> huffmanCode;
	encode(root, "", huffmanCode);

	cout << "Huffman Codes are :n" << 'n';
	for (auto pair: huffmanCode) {
		cout << pair.first << " " << pair.second << 'n';
	}

	cout << "nOriginal string was :n" << text << 'n';

	// print encoded string
	string str = "";
	for (char ch: text) {
		str += huffmanCode[ch];
	}

	cout << "nEncoded string is :n" << str << 'n';

	// traverse the Huffman Tree again and this time
	// decode the encoded string
	int index = -1;
	cout << "nDecoded string is: n";
	while (index < (int)str.size() - 2) {
		decode(root, index, str);
	}
}

// Huffman coding algorithm
int main()
{
	string text = "Huffman coding is a data compression algorithm.";

	buildHuffmanTree(text);

	return 0;
}

import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;

// A Tree node
class Node
{
	char ch;
	int freq;
	Node left = null, right = null;

	Node(char ch, int freq)
	{
		this.ch = ch;
		this.freq = freq;
	}

	public Node(char ch, int freq, Node left, Node right) {
		this.ch = ch;
		this.freq = freq;
		this.left = left;
		this.right = right;
	}
};

class Huffman
{
	// traverse the Huffman Tree and store Huffman Codes
	// in a map.
	public static void encode(Node root, String str,
							  Map<Character, String> huffmanCode)
	{
		if (root == null)
			return;

		// found a leaf node
		if (root.left == null && root.right == null) {
			huffmanCode.put(root.ch, str);
		}


		encode(root.left, str + "0", huffmanCode);
		encode(root.right, str + "1", huffmanCode);
	}

	// traverse the Huffman Tree and decode the encoded string
	public static int decode(Node root, int index, StringBuilder sb)
	{
		if (root == null)
			return index;

		// found a leaf node
		if (root.left == null && root.right == null)
		{
			System.out.print(root.ch);
			return index;
		}

		index++;

		if (sb.charAt(index) == '0')
			index = decode(root.left, index, sb);
		else
			index = decode(root.right, index, sb);

		return index;
	}

	// Builds Huffman Tree and huffmanCode and decode given input text
	public static void buildHuffmanTree(String text)
	{
		// count frequency of appearance of each character
		// and store it in a map
		Map<Character, Integer> freq = new HashMap<>();
		for (int i = 0 ; i < text.length(); i++) {
			if (!freq.containsKey(text.charAt(i))) {
				freq.put(text.charAt(i), 0);
			}
			freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
		}

		// Create a priority queue to store live nodes of Huffman tree
		// Notice that highest priority item has lowest frequency
		PriorityQueue<Node> pq = new PriorityQueue<>(
										(l, r) -> l.freq - r.freq);

		// Create a leaf node for each character and add it
		// to the priority queue.
		for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
			pq.add(new Node(entry.getKey(), entry.getValue()));
		}

		// do till there is more than one node in the queue
		while (pq.size() != 1)
		{
			// Remove the two nodes of highest priority
			// (lowest frequency) from the queue
			Node left = pq.poll();
			Node right = pq.poll();

			// Create a new internal node with these two nodes as children 
			// and with frequency equal to the sum of the two nodes
			// frequencies. Add the new node to the priority queue.
			int sum = left.freq + right.freq;
			pq.add(new Node('', sum, left, right));
		}

		// root stores pointer to root of Huffman Tree
		Node root = pq.peek();

		// traverse the Huffman tree and store the Huffman codes in a map
		Map<Character, String> huffmanCode = new HashMap<>();
		encode(root, "", huffmanCode);

		// print the Huffman codes
		System.out.println("Huffman Codes are :n");
		for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
			System.out.println(entry.getKey() + " " + entry.getValue());
		}

		System.out.println("nOriginal string was :n" + text);

		// print encoded string
		StringBuilder sb = new StringBuilder();
		for (int i = 0 ; i < text.length(); i++) {
			sb.append(huffmanCode.get(text.charAt(i)));
		}

		System.out.println("nEncoded string is :n" + sb);

		// traverse the Huffman Tree again and this time
		// decode the encoded string
		int index = -1;
		System.out.println("nDecoded string is: n");
		while (index < sb.length() - 2) {
			index = decode(root, index, sb);
		}
	}

	public static void main(String[] args)
	{
		String text = "Huffman coding is a data compression algorithm.";

		buildHuffmanTree(text);
	}
}

Примечание: память, используемая входной строкой, составляет 47 * 8 = 376 бит, а закодированная строка занимает всего 194 бита, т.е. данные сжимаются примерно на 48%. В программе на С++ выше мы используем класс string для хранения закодированной строки, чтобы сделать программу читаемой.

Поскольку эффективные структуры данных очереди приоритетов требуют на вставку O(log(N)) времени, а в полном бинарном дереве с N листьями присутствует 2N-1 узлов, и дерево Хаффмана – это полное бинарное дерево, то алгоритм работает за O(Nlog(N)) времени, где N – количество символов.

Источники:

en.wikipedia.org/wiki/Huffman_coding
en.wikipedia.org/wiki/Variable-length_code
www.youtube.com/watch?v=5wRPin4oxCo

Узнать подробнее о курсе.

Источник: habr.com