Прелюдия
Эта статья посвящена бинарным деревьям поиска. Недавно делал статью про Там я не очень обращал внимание на бинарные деревья, ибо методы поиска, вставки, удаления не были актуальны. Теперь решил написать статью именно про деревья. Пожалуй, начнем.
Дерево — структура данных, состоящая из узлов, соединенных ребрами. Можно сказать, что дерево — частный случай графа. Вот пример дерева:
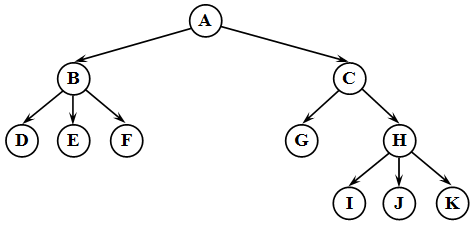
Это не бинарное дерево поиска! Все под кат!
Терминология
Корень
Корень дерева — это самый верхний его узел. В примере — это узел A. В дереве от корня к любому другому узлу может вести только один путь! На самом деле, любой узел можно рассматривать как корень соответствующего этому узлу поддерева.
Родители/потомки
Все узлы, кроме корневого, имеют ровно одно ребро, ведущее вверх к другому узлу. Узел, расположенный выше текущего, называется родителем этого узла. Узел, расположенный ниже текущего, и соединенный с ним называется потомком этого узла. Давайте на примере. Возьмем узел B, тогда его родителем будет узел A, а потомками — узлы D, E и F.
Лист
Узел, у которого нет потомков, будет называться листом дерева. В примере листьями будут являться узлы D, E, F, G, I, J, K.
Это основная терминология. Другие понятия будут разобраны далее. Итак, бинарное дерево — дерево, в котором каждый узел будет иметь не более двух потомков. Как вы догадались, дерево из примера не будет являться бинарным, ибо узлы B и H имеют более двух потомков. Вот пример бинарного дерева:
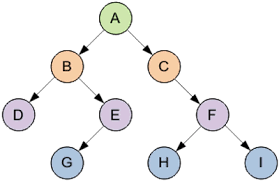
В узлах дерева может находиться любая информация. Двоичное дерево поиска — это двоичное дерево, для которого характерны следующие свойства:
- Оба поддерева — левое и правое — являются двоичными деревьями поиска.
- У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
- У всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равны, нежели значение ключа данных самого узла X.
Ключ — какая-либо характеристика узла(например, число). Ключ нужен для того, чтобы можно было найти элемент дерева, которому соответствует этот ключ. Пример бинарного дерева поиска:
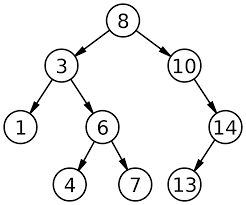
Представление дерева
По мере продвижения я буду приводить некоторые(возможно, неполные) куски кода, для того, чтобы улучшить ваше понимание. Полный код будет в конце статьи.
Дерево состоит из узлов. Структура узла:
public class Node<T> {
private T data;
private int key;
private Node<T> leftChild;
private Node<T> rightChild;
public Node(T data, int key) {
this.data = data;
this.key = key;
}
public Node<T> getLeftChild() {
return leftChild;
}
public Node<T> getRightChild() {
return rightChild;
}
//...остальные методы узла
}
Каждый узел имеет двух потомков(вполне возможно, потомки leftChild и/или rightChild будут содержать значение null). Вы, наверное, поняли, что в данном случае число data — данные, хранящиеся в узле; key — ключ узла.
С узлом разобрались, теперь поговорим о проблемах насущных о деревьях. Здесь и далее под словом «дерево» буду подразумевать понятие бинарного дерева поиска. Структура бинарного дерева:
public class BinaryTree<T> {
private Node<T> root;
//методы дерева
}
Как поле класса нам понадобится только корень дерева, ибо от корня с помощью методов getLeftChild() и getRightChild() можно добраться до любого узла дерева.
Алгоритмы в дереве
Поиск
Допустим, у вас есть построенное дерево. Как найти элемент с ключом key? Нужно последовательно двигаться от корня вниз по дереву и сравнивать значение key с ключом очередного узла: если key меньше, чем ключ очередного узла, то перейти к левому потомку узла, если больше — к правому, если ключи равны — искомый узел найден! Соответствующий код:
public Node<T> find(int key) {
Node<T> current = root;
while (current.getKey() != key) {
if (key < current.getKey())
current = current.getLeftChild();
else
current = current.getRightChild();
if (current == null)
return null;
}
return current;
}
Если current становится равным null, значит, перебор достиг конца дерева(на концептуальном уровне вы находитесь в несуществующем месте дерева — потомке листа).
Рассмотрим эффективность алгоритма поиска на сбалансированном дереве(дереве, в котором узлы распределены более-менее равномерно). Тогда эффективность поиска будет O(log(n)), причем логарифм по основанию 2. Смотрите: если в сбалансированном дереве n элементов, то это значит, что будет log(n) по основанию 2 уровней дерева. А в поиске, за один шаг цикла, вы спускаетесь на один уровень.
Вставка
Если вы уловили суть поиска, то понять вставку не составит вам труда. Надо просто спуститься до листа дерева(по правилам спуска, описанным в поиске) и стать его потомком — левым, или правым, в зависимости от ключа. Реализация:
public void insert(T insertData, int key) {
Node<T> current = root;
Node<T> parent;
Node<T> newNode = new Node<>(insertData, key);
if (root == null)
root = newNode;
else {
while (true) {
parent = current;
if (key < current.getKey()) {
current = current.getLeftChild();
if (current == null) {
parent.setLeftChild(newNode);
return;
}
}
else {
current = current.getRightChild();
if (current == null) {
parent.setRightChild(newNode);
return;
}
}
}
}
}
В данном случае надо, помимо текущего узла, хранить информацию о родителе текущего узла. Когда current станет равным null, в переменной parent будет лежать нужный нам лист.
Эффективность вставки, очевидно, будет такой же как и у поиска — O(log(n)).
Удаление
Удаление — самая сложная операция, которую надо будет провести с деревом. Понятно, что сначала надо будет найти элемент, который мы собираемся удалять. Но что потом? Если просто присвоить его ссылке значение null, то мы потерям информацию о поддереве, корнем которого является этот узел. Методы удаления дерева разделяют на три случая.
Первый случай. Удаляемый узел не имеет потомков
Если удаляемый узел не имеет потомков, то это значит, что он является листом. Следовательно, можно просто полям leftChild или rightChild его родителя присвоить значение null.
Второй случай. Удаляемый узел имеет одного потомка
Этот случай тоже не очень сложный. Вернемся к нашему примеру. Допустим, надо удалить элемент с ключом 14. Согласитесь, что так как он — правый потомок узла с ключом 10, то любой его потомок(в данном случае правый) будет иметь ключ, больший 10, поэтому можно легко его «вырезать» из дерева, а родителя соединить напрямую с потомком удаляемого узла, т.е. узел с ключом 10 соединить с узлом 13. Аналогичной была бы ситуация, если бы надо было удалить узел, который является левым потомком своего родителя. Подумайте об этом сами — точная аналогия.
Третий случай. Узел имеет двух потомков
Наиболее сложный случай. Разберем на новом примере.
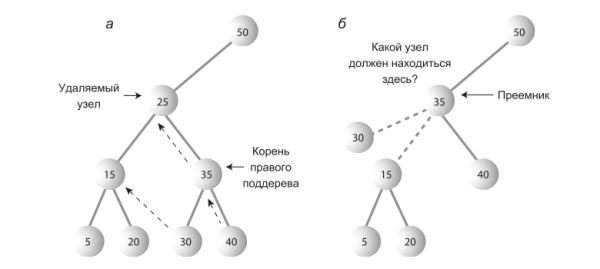
Поиск преемника
Допустим, надо удалить узел с ключом 25. Кого поставим на его место? Кто-то из его последователей(потомков или потомков потомков) должен стать преемником(тот, кто займет место удаляемого узла).
Как понять, кто должен стать преемником? Интуитивно понятно, что это узел в дереве, ключ которого — следующий по величине от удаляемого узла. Алгоритм заключается в следующем. Надо перейти к его правому потомку(всегда к правому, ибо уже говорилось, что ключ преемника больше ключа удаляемого узла), а затем пройтись по цепочке левых потомков этого правого потомка. В примере мы должны перейти к узлу с ключом 35, а затем пройтись до листа вниз по цепочке его левых потомков — в данном случае, эта цепочка состоит только из узла с ключом 30. Строго говоря, мы ищем наименьший узел в наборе узлов, больших искомого узла.
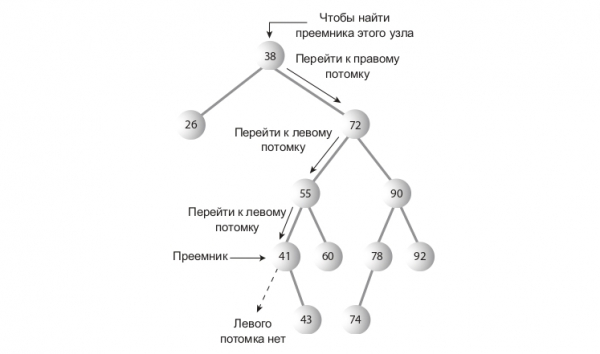
Код метода поиска преемника:
public Node<T> getSuccessor(Node<T> deleteNode) {
Node<T> parentSuccessor = deleteNode;//родитель преемника
Node<T> successor = deleteNode;//преемник
Node<T> current = successor.getRightChild();//просто "пробегающий" узел
while (current != null) {
parentSuccessor = successor;
successor = current;
current = current.getLeftChild();
}
//на выходе из цикла имеем преемника и родителя преемника
if (successor != deleteNode.getRightChild()) {//если преемник не совпадает с правым потомком удаляемого узла
parentSuccessor.setLeftChild(successor.getRightChild());//то его родитель забирает себе потомка преемника, чтобы не потерять его
successor.setRightChild(deleteNode.getRightChild());//связываем преемника с правым потомком удаляемого узла
}
return successor;
}
Полный код метода delete:
public boolean delete(int deleteKey) {
Node<T> current = root;
Node<T> parent = current;
boolean isLeftChild = false;//В зависимости от того, является ли удаляемый узел левым или правым потомком своего родителя, булевская переменная isLeftChild будет принимать значение true или false соответственно.
while (current.getKey() != deleteKey) {
parent = current;
if (deleteKey < current.getKey()) {
current = current.getLeftChild();
isLeftChild = true;
} else {
isLeftChild = false;
current = current.getRightChild();
}
if (current == null)
return false;
}
if (current.getLeftChild() == null && current.getRightChild() == null) {//первый случай
if (current == root)
current = null;
else if (isLeftChild)
parent.setLeftChild(null);
else
parent.setRightChild(null);
}
else if (current.getRightChild() == null) {//второй случай
if (current == root)
root = current.getLeftChild();
else if (isLeftChild)
parent.setLeftChild(current.getLeftChild());
else
current.setRightChild(current.getLeftChild());
} else if (current.getLeftChild() == null) {
if (current == root)
root = current.getRightChild();
else if (isLeftChild)
parent.setLeftChild(current.getRightChild());
else
parent.setRightChild(current.getRightChild());
}
else {//третий случай
Node<T> successor = getSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.setLeftChild(successor);
else
parent.setRightChild(successor);
}
return true;
}
Сложность может быть аппроксимирована к O(log(n)).
Поиск максимума/минимума в дереве
Очевидно, как найти минимальное/максимальное значение в дереве — надо последовательно переходить по цепочке левых/правых элементов дерева соответственно; когда доберетесь до листа, он и будет минимальным/максимальным элементом.
public Node<T> getMinimum(Node<T> startPoint) {
Node<T> current = startPoint;
Node<T> parent = current;
while (current != null) {
parent = current;
current = current.getLeftChild();
}
return parent;
}
public Node<T> getMaximum(Node<T> startPoint) {
Node<T> current = startPoint;
Node<T> parent = current;
while (current != null) {
parent = current;
current = current.getRightChild();
}
return parent;
}
Сложность — O(log(n))
Симметричный обход
Обход — посещение каждого узла дерева с целью сделать с ним какое-то действие.
Алгоритм рекурсивного симметричного обхода:
- Сделать действие с левым потомком
- Сделать действие с собой
- Сделать действие с правым потомком
Код:
public void inOrder(Node<T> current) {
if (current != null) {
inOrder(current.getLeftChild());
System.out.println(current.getData() + " ");//Здесь может быть все, что угодно
inOrder(current.getRightChild());
}
}
Заключение
Наконец-то! Если я что-то недообъяснил или есть какие-либо замечания, то жду в комментариях. Как обещал, привожу полный код.
Node.java:
public class Node<T> {
private T data;
private int key;
private Node<T> leftChild;
private Node<T> rightChild;
public Node(T data, int key) {
this.data = data;
this.key = key;
}
public void setLeftChild(Node<T> newNode) {
leftChild = newNode;
}
public void setRightChild(Node<T> newNode) {
rightChild = newNode;
}
public Node<T> getLeftChild() {
return leftChild;
}
public Node<T> getRightChild() {
return rightChild;
}
public T getData() {
return data;
}
public int getKey() {
return key;
}
}
BinaryTree.java:
public class BinaryTree<T> {
private Node<T> root;
public Node<T> find(int key) {
Node<T> current = root;
while (current.getKey() != key) {
if (key < current.getKey())
current = current.getLeftChild();
else
current = current.getRightChild();
if (current == null)
return null;
}
return current;
}
public void insert(T insertData, int key) {
Node<T> current = root;
Node<T> parent;
Node<T> newNode = new Node<>(insertData, key);
if (root == null)
root = newNode;
else {
while (true) {
parent = current;
if (key < current.getKey()) {
current = current.getLeftChild();
if (current == null) {
parent.setLeftChild(newNode);
return;
}
}
else {
current = current.getRightChild();
if (current == null) {
parent.setRightChild(newNode);
return;
}
}
}
}
}
public Node<T> getMinimum(Node<T> startPoint) {
Node<T> current = startPoint;
Node<T> parent = current;
while (current != null) {
parent = current;
current = current.getLeftChild();
}
return parent;
}
public Node<T> getMaximum(Node<T> startPoint) {
Node<T> current = startPoint;
Node<T> parent = current;
while (current != null) {
parent = current;
current = current.getRightChild();
}
return parent;
}
public Node<T> getSuccessor(Node<T> deleteNode) {
Node<T> parentSuccessor = deleteNode;
Node<T> successor = deleteNode;
Node<T> current = successor.getRightChild();
while (current != null) {
parentSuccessor = successor;
successor = current;
current = current.getLeftChild();
}
if (successor != deleteNode.getRightChild()) {
parentSuccessor.setLeftChild(successor.getRightChild());
successor.setRightChild(deleteNode.getRightChild());
}
return successor;
}
public boolean delete(int deleteKey) {
Node<T> current = root;
Node<T> parent = current;
boolean isLeftChild = false;
while (current.getKey() != deleteKey) {
parent = current;
if (deleteKey < current.getKey()) {
current = current.getLeftChild();
isLeftChild = true;
} else {
isLeftChild = false;
current = current.getRightChild();
}
if (current == null)
return false;
}
if (current.getLeftChild() == null && current.getRightChild() == null) {
if (current == root)
current = null;
else if (isLeftChild)
parent.setLeftChild(null);
else
parent.setRightChild(null);
}
else if (current.getRightChild() == null) {
if (current == root)
root = current.getLeftChild();
else if (isLeftChild)
parent.setLeftChild(current.getLeftChild());
else
current.setRightChild(current.getLeftChild());
} else if (current.getLeftChild() == null) {
if (current == root)
root = current.getRightChild();
else if (isLeftChild)
parent.setLeftChild(current.getRightChild());
else
parent.setRightChild(current.getRightChild());
}
else {
Node<T> successor = getSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.setLeftChild(successor);
else
parent.setRightChild(successor);
}
return true;
}
public void inOrder(Node<T> current) {
if (current != null) {
inOrder(current.getLeftChild());
System.out.println(current.getData() + " ");
inOrder(current.getRightChild());
}
}
}
P.S.
Вырождение до O(n)
Многие из вас могли заметить: а что, если сделать так, чтобы дерево стало несбалансированным? Например, класть в дерево узлы с возрастающими ключами: 1,2,3,4,5,6… Вот тогда дерево будет чем-то напоминать связный список. И да, дерево потеряет свою древовидную структуру, а следовательно, и эффективность доступа к данным. Сложность операций поиска, вставки, удаления станут такими, как у связного списка: O(n). В этом и проявляется один из важнейших, на мой взгляд, недостатков бинарных деревьев.
Только зарегистрированные пользователи могут участвовать в опросе. , пожалуйста.
Я не совсем давно на хабре, и мне хотелось бы знать, статьи на какие темы хотели бы вы видеть больше?
Структуры данных
Алгоритмы(ДП, рекурсия, сжатие данных и т. д.)
Применение структур данных и алгоритмов в реальной жизни
Программирование android-приложений на Java
Программирование web-приложений на Java
Проголосовали 2 пользователя. Воздержался 1 пользователь.
Источник: habr.com


