 В прошлых частях (, ) мы говорили о глобалах как о деревьях, в этой мы рассмотрим глобалы как разреженные массивы.
В прошлых частях (, ) мы говорили о глобалах как о деревьях, в этой мы рассмотрим глобалы как разреженные массивы.
— это разновидность массива, в котором большинство значений принимает одинаковое значение.
На практике часто встречаются настолько огромные разреженные массивы, что нет никакого смысла занимать память одинаковыми элементами. Поэтому есть смысл разреженные массивы реализовывать так, чтобы память не расходовалась на хранение одинаковых значений.
В некоторых языках программирования разреженные массивы входят в сам язык, , . В других языках программирования есть специальные библиотеки, которые позволяют реализовать их. Для С++ — и др.
Глобалы — хорошие кандидаты для реализации разреженных массивов, потому что:
- Хранят значения только определённых узлов и не хранят значения неопределённых;
- Интерфейс доступа к значению узла чрезвычайно похож на то, как во многих языках программирования реализован доступ к элементу многомерного массива.
Set ^a(1, 2, 3)=5 Write ^a(1, 2, 3) - Глобал — достаточно низкоуровневая структура для хранения данных, поэтому обладают выдающими скоростными характеристиками (от сотен тысяч до десятков миллионов транзакций в секунду в зависимости от железа, см. )
Поскольку глобал — персистентная структура, то разреженные массивы делать на них имеет смысл тогда, когда заранее известно, что объёма оперативной памяти будет недостаточно.
Одним из свойств реализаций разреженных массивов является возврат некоторого значения по-умолчанию, если обращение ведётся к неопределённой ячейке.
Это можно реализовать, используя функцию в COS. В данном примере рассмотрен 3-х мерный массив.
SET a = $GET(^a(x,y,z), defValue)В каких же задачах требуются разреженные массивы и как глобалы могут выручить?
Матрица смежности (связности)
используются для представления графов:
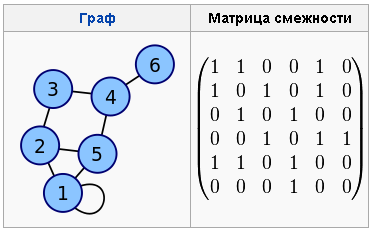
Очевидно, что чем больше граф, тем больше нулей будет в матрице. Если, например, взять граф социальной сети и представить его в виде подобной матрицы, то он почти весь будет состоять из нулей, т.е. будет разреженным массивом.
Set ^m(id1, id2) = 1
Set ^m(id1, id3) = 1
Set ^m(id1, id4) = 1
Set ^m(id1) = 3
Set ^m(id2, id4) = 1
Set ^m(id2, id5) = 1
Set ^m(id2) = 2
....
В данном примере мы сохраняем в глобале ^m матрицу связности, а также число ребёр у каждого узла (кто с кем дружит и число друзей).
Если же число элементов в графе не более 29 миллионов (это число берётся как произведение 8 * ), то есть ещё более экономичный способ хранения таких матриц — битовые строки, так как в их реализации специальным образом оптимизируются большие пропуски.
Манипуляции с битовыми строками производятся функцией .
; установка бита
SET $BIT(rowID, positionID) = 1
; получение бита
Write $BIT(rowID, positionID)
Таблица переходов конечного автомата
Поскольку граф переходов конечного автомата — это обыкновенный граф, то и таблица переходов конечного автомата — это та же самая матрица смежности, о которой говорилось выше.
Клеточные автоматы

Самый известный клеточный автомат — , который из-за своих правил (когда у клетки много соседей — она умирает) представляет собой разреженный массив.
Стивен Вольфрам, считает что клеточные автоматы — это . В 2002 году он публикует 1280-страничную книгу «A New Kind of Science», где широко аргументирует, что достижения в области клеточных автоматов не являются изолированными, но весьма устойчивы и имеют большое значение для всех областей науки.
Доказано, что любой алгоритм выполнимый на компьютере можно реализовать посредством клеточного автомата. Клеточные автоматы используются для моделирования динамических сред и систем, для решений алгоритмических задач и других целей.
Если у нас огромное поле и нам нужно записывать все промежуточные состояния клеточного автомата, то вполне разумно использовать глобалы.
Картография
Первое что приходит мне на ум, когда речь идёт об использовании разреженных массивов — это картографические задачи.
Как правило на картах очень много пустого пространства. Если карту представлять в виде больших пикселов, то 71% пикселов Земли будет занято океаном. Разреженный массив. А если наносить только произведения рук человеческих, то пустого пространства будет более 95%.
Конечно, никто не хранит карты в виде растровых массивов, используется векторное представление.
Но что из себя представляют векторные карты? Это некая рамка и состоящие из точек полилинии и полигоны.
Фактически база данных точек и связей между ними.
Одна из самых амбициозных задач картирования — это миссия картирования нашей галактики телескопом Гайя. Образно говоря, наша галактика, как и вся вселенная есть сплошной разреженный массив: огромные пространства пустоты, в которых есть редкие маленькие точки — звёзды. Пустого места 99,999999…….%. Для хранения карты нашей галактики была выбрана база данных на глобалах — Caché.
Я не знаю точную структуру глобалов в этом проекте, могу предположить, что это что-то похожее на:
Set ^galaxy(b, l, d) = 1; Номер звезды по каталогу, если есть
Set ^galaxy(b, l, d, "name") = "Sun"
Set ^galaxy(b, l, d, "type") = "normal" ; варианты blackhole, quazar, red_dwarf и т.д.
Set ^galaxy(b, l, d, "weight") = 14E50
Set ^galaxy(b, l, d, "planetes") = 7
Set ^galaxy(b, l, d, "planetes", 1) = "Mercury"
Set ^galaxy(b, l, d, "planetes", 1, weight) = 1E20
...
Где b, l, d — это и расстояние до Солнца.
Гибкая структура глобалов позволяет сохранить любые нужные характеристики звёзд и планет, так как базы на глобалах бессхемные (scheme-less).
Для хранения карты нашей вселенной Caché была выбрана не только из-за гибкости, но и из-за способности очень быстро сохранять поток данных, при этом попутно создавая индексные глобалы для быстрого поиска.
Если же вернуться к Земле, то на глобалах были созданы картографические проекты и форк OpenStreetMap — .
Недавно на были реализованы геопространственные индексы . Ждём от авторов статьи с деталями реализации.
Реализация пространственных индексов на глобале в OpenStreetMap XAPI
Картинки взяты из .
Весь земной шар разбивается на квадратики, потом подквадратики, а подквадратики на подподквадратики и так далее. В общем получаем иерархическую структуру для хранения которых и созданы глобалы.

В любой момент мы можем практически моментально затребовать нужный квадрат или его очистить, при этом все подквадратики также будут возвращены или очищены.
Подобную схему на глобалах можно реализовать несколькими способами.
Вариант 1:
Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 1) = idПервойТочки
Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 2) = idВторойТочки
...Вариант 2:
Set ^m('abacdabcdabacdabcda', 1) = idПервойТочки
Set ^m('abacdabcdabacdabcda', 2) = idВторойТочки
...В обоих случаях не составляет труда на COS/M затребовать точки находящиеся в квадрате любого уровня. Несколько легче будет очищать квадратные куски пространства любого уровня в первом варианте, но это редко нужно.
Пример одного из квадратиков нижнего уровня:

А вот несколько глобалов из проекта XAPI: представление индекса на глобалах:

Глобал ^way используется для хранения точек (дорог, мелких рек и т.п.) и полигонов (замкнутые области: здания, леса и т.д.).
Грубая классификация использования разреженных массивов на глобалах.
- Мы храним координаты неких объектов и их состояния (картирование, клеточные автоматы)
- Мы храним разреженные матрицы.
Для случая 2) при запросе определённой координаты, где элементу не присвоено значение, мы должны получить значение элемента разреженного массива по умолчанию.
Бонусы, которые мы получаем при хранении многомерных матриц в глобалах
Быстрое удаление и/или выборки кусков пространства, кратных строкам, плоскостям, кубам и т.д. Для случаев, когда используются целочисленные индексы, может оказаться полезной возможность быстрого удаления и/или выборки кусков пространства, кратных строкам, плоскостям, кубам и т.д.
Командой мы можем удалить как отдельный элемент, так и строку, и даже целую плоскость. Благодаря свойствам глобалов, это происходит очень быстро — в тысячи раз быстрее, чем поэлементное удаление.
На рисунке показан трёхмерный массив в глобале ^a и разные виды удалений.
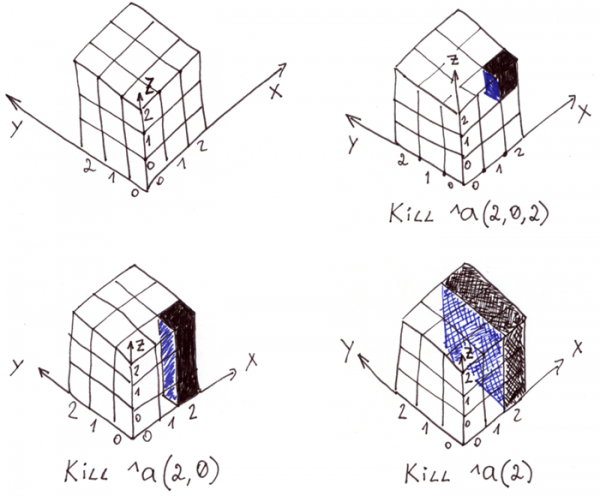
Для выборки кусков пространства по известным индексам можно использовать команду .
Выборка столбца матрицы в переменную Column:
; Зададим трёхмерный разреженный массив 3x3x3
Set ^a(0,0,0)=1,^a(2,2,0)=1,^a(2,0,1)=1,^a(0,2,1)=1,^a(2,2,2)=1,^a(2,1,2)=1
Merge Column = ^a(2,2)
; Выведем переменную Column
Zwrite Column
Вывод:
Column(0)=1
Column(2)=1
Что интересно в переменной Column у нас тоже получился разреженный массив, к которому обращаться нужно тоже через , так как значения по умолчанию в нём не хранятся.
Выборка кусков пространства также может делаться через небольшую программу с использование функции . Это в особенности удобно на пространствах, индексы которых неквантованы (картография).
Заключение
Нынешние времена ставят новые амбициозные задачи. Графы могут состоять из миллиардов вершин, карты из миллиардов точек, а кто-то даже может захотеть запустить свою собственную вселенную на клеточных автоматах (, ).
Когда объём данных разреженных массивов уже никак не может быть вмещён в оперативную память, а работать с ними нужно, то стоит рассмотреть возможность реализации подобных проектов на глобалах и COS.
Спасибо за внимание! Ждём ваших вопросов и пожеланий в комментариях.
Disclaimer: данная статья и мои комментарии к ней является моим мнением и не имеют отношения к официальной позиции корпорации InterSystems.
Источник: habr.com



