Можно ли генерировать случайные числа, если мы не доверяем друг другу? Часть 2

Привет, Хабр!

В первой части статьи мы обсудили, зачем может быть необходимо генерировать случайные числа участникам, которые не доверяют друг другу, какие требования выдвигаются к таким генераторам случайных чисел, и рассмотрели два подхода к их реализации.

В этой части статьи мы подробно рассмотрим еще один подход, который использует пороговые подписи.

Немного криптографии

Для того, чтобы понять, как работают пороговые подписи, надо понимать немного базовой криптографии. Мы будем использовать две концепции: скаляры, или просто числа, которые мы будем обозначать строчными буквами (x, y) и точки на эллиптической кривой, которые мы будем обозначать прописными буквами.

Для понимания основ пороговых подписей не надо понимать как работают эллиптические кривые, кроме нескольких базовых вещей:

1. Точки на эллиптической кривой можно складывать и умножать на скаляр (умножение на скаляр мы будем обозначать как xG, хотя нотация Gx тоже часто используется в литературе). Результат сложения и умножения на скаляр — это точка на эллиптической кривой.

2. Зная только точку G и ее произведение со скаляром xG нельзя вычислить x.

Мы будем также использовать концепцию полинома p(x) степени k-1. В частности, мы будем использовать следующее свойство полиномов: если мы знаем значение p(x) для любых k различных x (и не имеем больше никакой информации о p(x)), мы можем вычислить p(x) для любого другого x.

Интересно, что для любого полинома p(x) и некоторой точки на кривой G, зная значение p(x)G для любых k различных значений x, можно также вычислить p(x)G для любой x.

Этой информации достаточно для того, чтобы закопаться в детали того, как работают пороговые подписи, и как их использовать для генерации случайных чисел.

Генератор случайных чисел на пороговых подписях

Допустим что n участников хотят сгенерировать случайное число, и мы хотим, чтобы участие любых k из них было достаточно чтобы сгенерировать число, но чтобы злоумышленники, которые контролируют k-1 или меньше участников, не могли предсказать или повлиять на сгенерированное число.

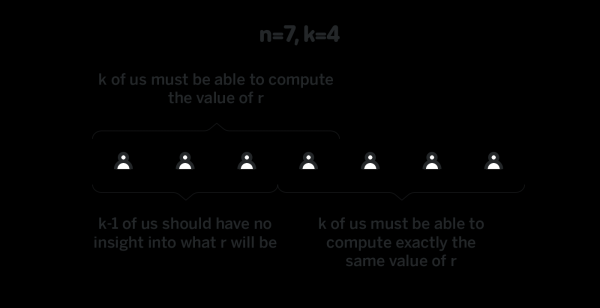
Допустим существует такой полином p(x) степени k-1, что первый участник знает p(1), второй знает p(2), и так далее (n-ый знает p(n)). Также допустим, что для некоторой заранее определенной точки G все знают p(x)G для всех значений x. Мы будем называть p(i) “приватной компонентой” i-ого участника (потому что только i-ый участник знает ее), и p(i)G “публичной компонентой” i-ого участника (потому что все участники знают ее). Как вы помните, знание p(i)G не достаточно чтобы восстановить p(i).

Создание такого полинома так, чтобы только i-ый участник и никто другой знал свою приватную компоненту – это самая сложная и интересная часть протокола, и мы разберем ее ниже. Пока допустим, что такой полином у нас есть, и все участники знают свои приватные компоненты.

Как мы можем использовать такой полином, чтобы сгенерировать случайное число? Для начала нам нужно некоторая строка, которая прежде не использовалась как вход для генератора. В случае блокчейна хеш последнего блока h — хороший кандидат для такой строки. Пусть участники хотят создать случайное число, используя h как seed. Сначала участники конвертируют h в точку на кривой используя любую заранее определенную функцию:

H = scalarToPoint(h)

Затем каждый участник i вычисляет и публикует Hi = p(i)H, что они могут сделать, потому что они знают p(i) и H. Раскрытие Hi не позволяет другим участникам восстановить приватную компоненту i-ого участника, и поэтому один набор приватных компонент можно использовать от блока к блоку. Таким образом, дорогой алгоритм создания полинома, описанный ниже, необходимо выполнить только однажды.

Когда k участников вскрыли Hi = p(i)H, все могут вычислить Hx = p(x)H для всех x благодаря свойству полиномов, которые мы обсудили в прошлом разделе. В этот момент все участники вычисляют H0 = p(0)H, и это и есть результирующее случайное число. Обратите внимание, что никто не знает p(0), и следовательно единственный способ посчитать p(0)H – это интерполяция p(x)H, что возможно только когда k значений p(i)H известны. Вскрытие любого меньшего количества p(i)H не дает никакой информации о p(0)H.

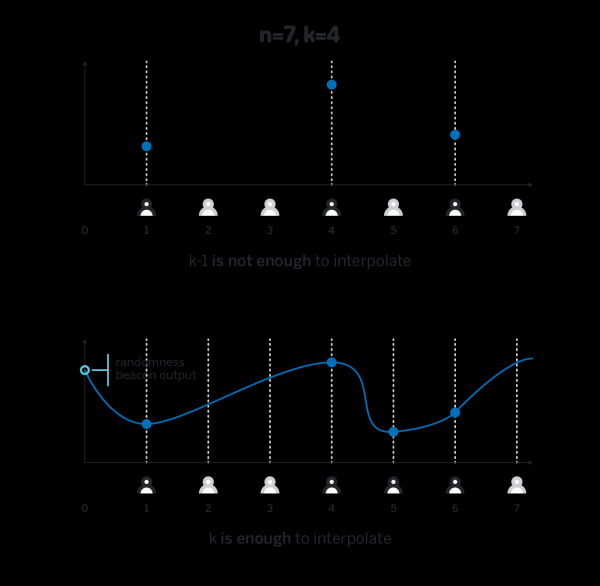
Генератор выше имеет все свойства, которые мы хотим: злоумышленники, контролирующие только k-1 участников, или меньше, не имеют никакой информации и влияния на вывод, в то время как любые k участников могут вычислить результирующее число, и любое подмножество из k участников всегда придут к одному и тому же результату для одного и того же seed.

Есть одна проблема, которую мы аккуратно обошли стороной выше. Чтобы интерполяция работала, важно чтобы значение Hi которое опубликовал каждый участник i действительно было равно p(i)H. Так как никто кроме i-ого участник не знает p(i), никто кроме i-ого участника не может проверить что Hi действительно посчитано правильно, и без какого-то криптографического доказательства корректности Hi злоумышленник может опубликовать любое значение в качестве Hi, и произвольно влиять на вывод генератора случайных чисел:

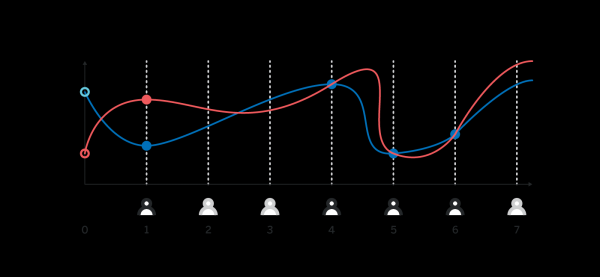Разные значения H_1, отправленные первым участником, приводят к разным результирующим H_0

Есть по меньшей мере два способа доказать корректность Hi, мы их рассмотрим после того, как разберем генерацию полинома.

Генерация полинома

В прошлом разделе мы допустили, что у нас есть такой полином p(x) степени k-1 что участник i знает p(i), и никто другой не имеет никакой информации об этом значении. В следующем разделе нам также будет необходимо чтобы для некоторой заранее определенной точки G все знали p(x)G для всех x.

В этом разделе мы будем полагать, что каждый участник имеет локально некоторый приватный ключ xi, такой что всем известен соответствующий публичный ключ Xi.

Один возможный протокол генерации полинома следующий:

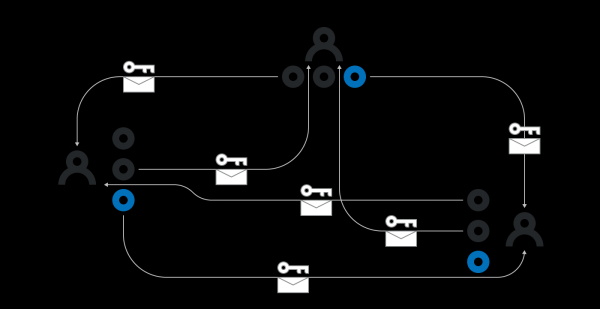
1. Каждый участник i локально создает произвольный полином pi(x) степени k-1. Они затем посылают каждому участнику j значение pi(j), зашифрованное публичным ключом Xj. Таким образом только i-ый и j-ый участник знают pi(j). Участник i также публично анонсирует pi(j)G для всех j от 1 до k включительно.

2. Все участники используют некоторый консенсус чтобы выбрать k участников, чьи полиномы будут использоваться. Так как некоторые участники могут быть оффлайн, мы не можем ждать пока все n участников опубликуют полиномы. Результат этого шага – множество Z состоящее из хотя бы k полиномов, созданных на шаге (1).

3. Участники убеждаются, что известные им значения pi(j) соответствуют публично анонсированным pi(j)G. После этого шага в Z должны остаться только полиномы, для которых приватно переданные pi(j) соответствуют публично анонсированным pi(j)G.

4. Каждый участник j вычисляет свою приватную компоненту p(j) как сумму pi(j) для всех i в Z. Каждый участник также вычисляет все значения p(x)G как сумму pi(x)G для всех i в Z.

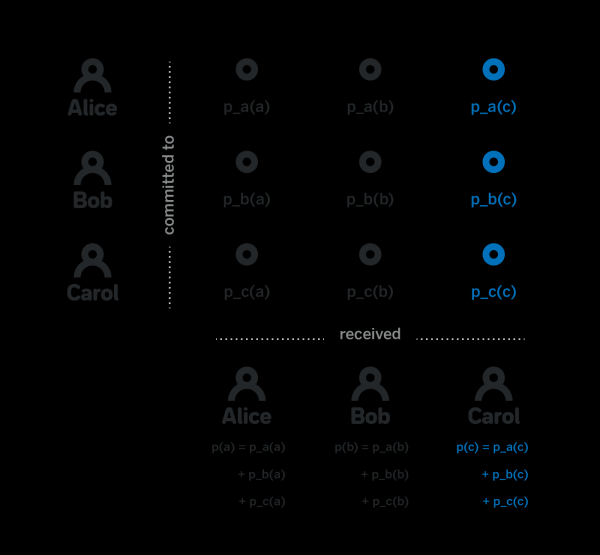
Обратите внимание, что p(x) – это действительно полином степени k-1, потому что это сумма отдельных pi(x), каждый из которых – это полином степени k-1. Затем, обратите внимание, что в то время как каждый участник j знает p(j), у них нет никакой информации об p(x) для x ≠ j. Действительно, чтобы вычислить это значение, им необходимо знать все pi(x), и покуда участник j не знает хотя бы один из выбранных полиномов, у них нет достаточной информации об p(x).

Это весь процесс генерации полинома, который был необходим в прошлом разделе. Шаги 1, 2 и 4 выше имеют достаточно очевидную реализацию. А вот шаг 3 не такой тривиальный.

Конкретно, нам нужно уметь доказывать, что зашифрованные pi(j) действительно соответствуют опубликованным pi(j)G. Если мы не можем это доказать, злоумышленник i может послать мусор вместо pi(j) участнику j, и участник j не сможет получить настоящее значение pi(j), и не сможет вычислить свою приватную компоненту.

Есть криптографический протокол, который позволяет создать дополнительное сообщение proofi(j), такое что любой участник, имея некоторое значение e, а также proofi(j) и pi(j)G, может локально убедиться, что e – это действительно pi(j), зашифрованное ключом участника j. К сожалению, размер такого доказательства невероятно большой, и учитывая что необходимо опубликовать O(nk) таких доказательств, использовать их для этой цели не получится.

Вместо того, чтобы доказывать, что pi(j) соответствует pi(j)G мы можем в протоколе генерации полинома отвести очень большой промежуток времени, во время которого все участники проверяют полученные зашифрованные pi(j), и если расшифрованное сообщение не соответствует публичному pi(j)G, они публикуют криптографическое доказательство того, что полученное ими зашифрованное сообщение неверно. Доказать, что сообщение не соответствует pi(G) намного проще, чем доказать, что оно соответствует. Следует отметить, что это требует, чтобы каждый участник появился в сети хотя бы раз за время, отведенное на создание таких доказательств, и полагается на предположение, что если они такое доказательство опубликовали, оно достигнет всех остальных участников за это же отведенное время.

Если участник не появился в сети в этот период времени, и у него действительно была хотя бы одна некорректная компонента, то этот конкретный участник не сможет участвовать в дальнейшей генерации чисел. Протокол, однако, все еще будет функционировать, если есть хотя бы k участников, которые либо только получили корректные компоненты, либо успели оставить доказательство некорректности в отведенное время.

Доказательства корректности H_i

Последняя часть, которую осталось обсудить, это как доказать корректность опубликованных Hi, а именно что Hi = p(i)H, без вскрытия p(i).

Вспомним, что значения H, G, p(i)G публичны и известны всем. Операция получения p(i) зная p(i)G и G называется дискретный логарифм, или dlog, и мы хотим доказать, что:

dlog(p(i)G, G) = dlog(Hi, H)

без разглашения p(i). Конструкции для таких доказательств существуют, например Schnorr Protocol.

С такой конструкцией, каждый участник вместе с Hi отправляет доказательство корректности согласно конструкции.

Когда случайное число сгенерировано, его часто нужно использовать участникам, отличным от тех, кто его сгенерировал. Таким участникам вместе с числом необходимо отправлять все Hi и сопутствующие доказательства.

Пытливый читатель может спросить: так как финальное случайное число – это H0, и p(0)G – это публичная информация, зачем нужно доказательство для каждого отдельного Hi, почему вместо этого не отправить доказательство того, что

dlog(p(0)G, G) = dlog(H0, H)

Проблема, что с помощью Schnorr Protocol нельзя создать такое доказательство, потому что никто не знает значение p(0), необходимое для создания доказательства, и более того, весь генератор случайных чисел основан на том, что никто не знает это значение. Поэтому необходимо иметь все значения Hi и их индивидуальные доказательства, чтобы доказать корректность H0.

Однако, если бы на точках на эллиптических кривых была бы какая-то операция, которая семантически схожа с умножением, доказательство корректности H0 было бы тривиальным, мы бы просто убедились, что

H0 × G = p(0)G × H

Если выбранная кривая поддерживает elliptic curve pairings, такое доказательство работает. В этом случае H0 – это не только вывод генератора случайных чисел, который может проверить любой участник, который знает G, H и p(0)G. H0 – это еще и подпись на сообщении, которое использовалось как seed, подтверждающая, что k и n участников подписали это сообщение. Таким образом, если seed – это хеш блока в протоколе блокчейна, то H0 – это одновременно мульти-подпись на блоке, и очень хорошее случайное число.

В заключение

Эта статья – часть серии технических статей в блоге NEAR. NEAR – это блокчейн протокол и платформа для разработки децентрализованных приложений с акцентом на простоту разработки, и простоту использования для конечных пользователей.

Код протокола открыт, наша реализация написана на Rust, её можно найти тут.

Посмотреть как выглядит разработка под NEAR, и поэкспериментировать в онлайн-IDE можно здесь.

Следить за всеми новостями на русском можно в группе в телеграме и в группе на ВКонтакте, а на английском в официальном твиттере.

До скорых встреч!

Источник: habr.com