Очистка данных, как игра «Камень, Ножницы, Бумага». Это игра с финишем или без? Часть 2. Практическая

В части первой описывалось, что данная публикация сделана на основе датасета результатов кадастровой оценки объектов недвижимости в Ханты-Мансийском АО.

Практическая часть представлена в виде шагов. Проводилась вся очистка в Excel, так как самый распространенный инструмент и описанные операции может повторить большинство специалистов знающих Excel. И достаточно неплохо подходит для работы в «рукопашную».

Нулевым этапом поставлю работы по запуску, сохранению файла, так как он размером 100 мб, то при количестве этих операций десятки и сотни на них уходит существенное время.
Открытие, в среднем, — 30 сек.
Сохранение – 22 сек.

Первый этап начинается с определения статистических показателей датасета.

Таблица 1. Статпоказатели датасета

Технология 2.1.

Создаем вспомогательное поле, у меня оно под номером — AY. Для каждой записи формируем формулу «=ДЛСТР(F365502)+ДЛСТР(G365502)+…+ДЛСТР(AW365502)»

Общее время, потраченное на этап 2.1 (для формулы Шумана) t21 = 1 час.
Количество найденных ошибок на этапе 2.1 (для формулы Шумана) n21 = 0 шт.

Второй этап.
Проверка комплектующих датасета.
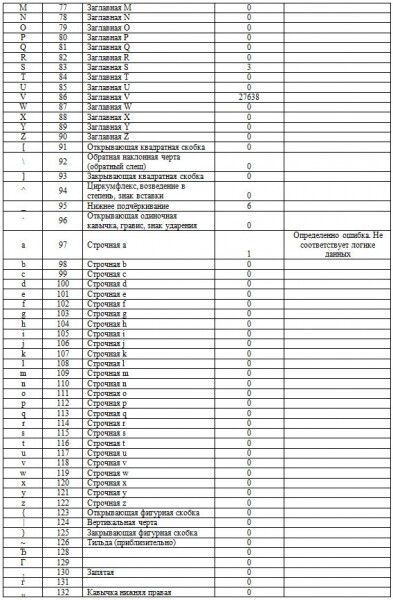
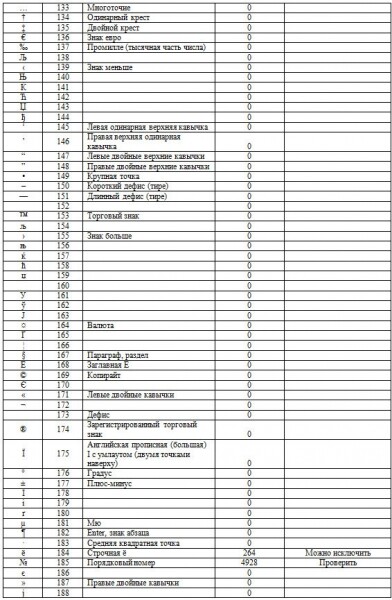
2.2. Все значения в записях формируются стандартными символами. Поэтому отследим статистику по символам.

Таблица 2. Статпоказатели символов в датасете с предварительным анализом результатов.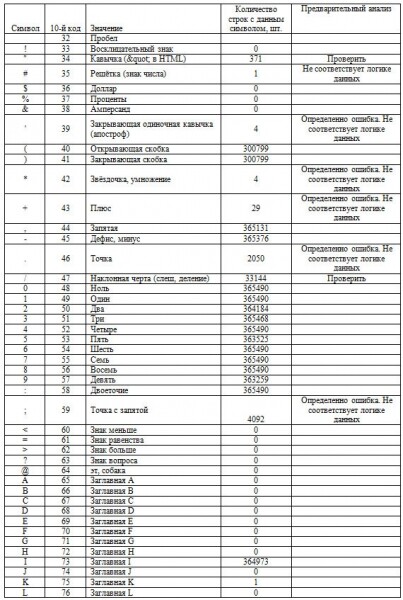





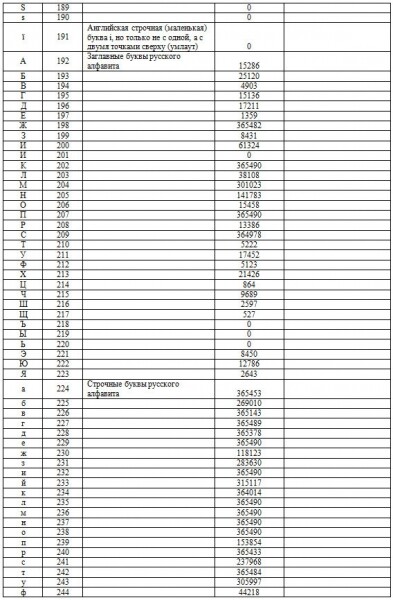
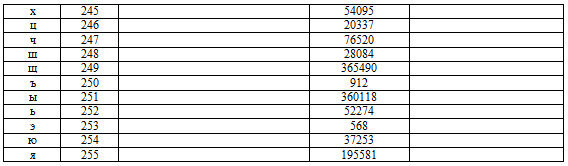
Технология 2.2.1.

Создаем вспомогательное поле – «альфа1». Для каждой записи формируем формулу «=СЦЕПИТЬ(Лист1!B9;…Лист1!AQ9)»
Создаем фиксированную ячейку «Омега-1». В эту ячейку поочередно будем вносить коды символов по Windows-1251 от 32 до 255.
Создаем вспомогательное поле – «альфа2». С формулой «=НАЙТИ(СИМВОЛ(Омега;1); «альфа1»;N)».
Создаем вспомогательное поле – «альфа3». С формулой «=ЕСЛИ(ЕЧИСЛО(«альфа2»;N);1;0)»
Создаем фиксированную ячейку «Омега-2», с формулой «=СУММ(«альфа3»N1: «альфа3»N365498)»

Таблица 3. Результаты предварительным анализом результатов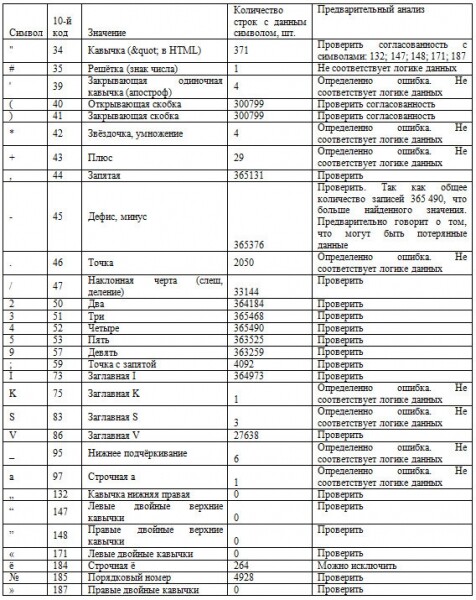

Таблица 4. Зафиксированные ошибки на данном этапе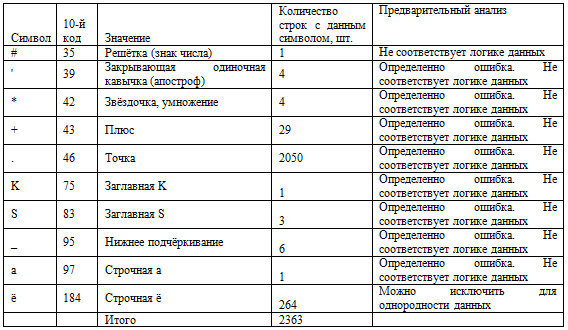

Общее время, потраченное на этап 2.2.1 (для формулы Шумана) t221 = 8 час.
Количество исправленных ошибок на этапе 2.2.1 (для формулы Шумана) n221 = 0 шт.

Этап 3.
Третьим этапом зафиксируем состояние датасета. Путем присваивания каждой записи уникального номера (ID) и каждому полю. Это необходимо для сопоставления преобразованного датасета с первоначальным. Также это необходимо, чтобы в полном объеме использоваться возможности группировок и фильтрациия. Здесь опять обращаемся к таблице 2.2.2 и выбираем символ, который в датасете не используется. Получаем показанное на рисунке 10.

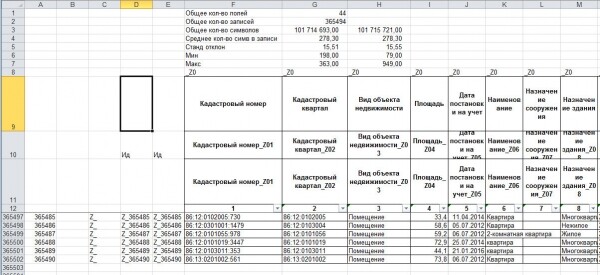
Рис.10. Присваивание идентификаторов.

Общее время, потраченное на этап 3 (для формулы Шумана) t3 = 0,75 час.
Количество найденных ошибок на этапе 3 (для формулы Шумана) n3 = 0 шт.

Так как для формулы Шумана необходимо, чтобы этап был завершен исправлением ошибок. Возвращаемся к этапу 2.

Этап 2.2.2.
В этом этапе исправим также двойные и тройные пробелы.

Рис.11. Количество двойных пробелов.

Исправление определённых в таблице 2.2.4 ошибок.

Таблица 5. Этап исправления ошибок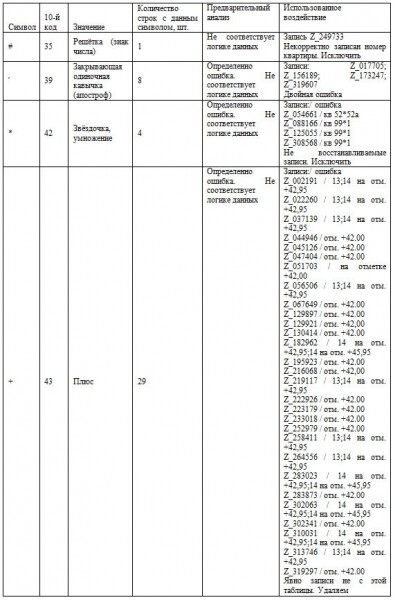


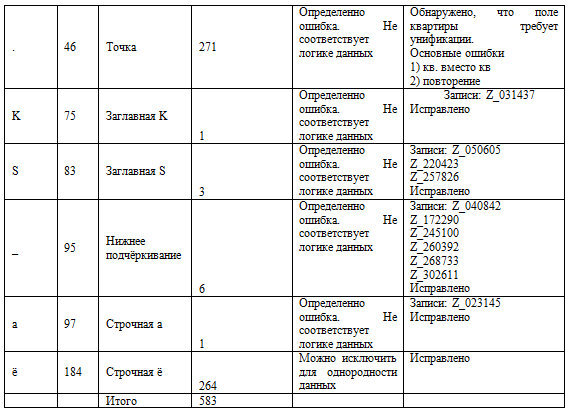
Пример того почему такой аспект как использование букв «е» или «ё» существенен представлен на рисунке 12.

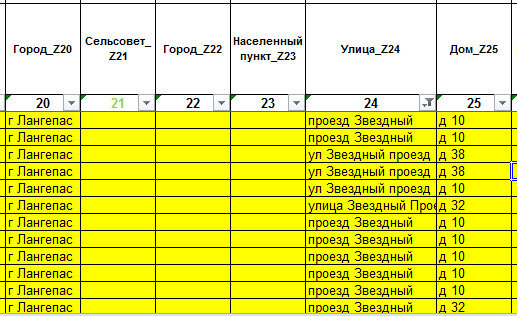
Рис.12. Разнобой по букве «ё».

Общее время, потраченное на этапе 2.2.2 t222 = 4 часа.
Количество найденных ошибок на этапе 2.2.2 (для формулы Шумана) n222 = 583 шт.

Четвертый этап.
В данный этап хорошо вписывается проверка на избыточность полей. Из 44 полей 6 полей:
7 — Назначение сооружения
16 — Количество подземных этажей
17 — Родительский объект
21 — Сельсовет
38 — Параметры сооружения (описание)
40 — Культурное наследие

Не имеют ни одной записи. То есть избыточны.
Поле «22 – Город» имеет одну единственную запись, рисунок 13.

Рис.13. Единственная запись Z_348653 в поле «Город».

Поле «34 — Наименование здания» несут записи явно не соответствующие назначению поля, рисунок 14.

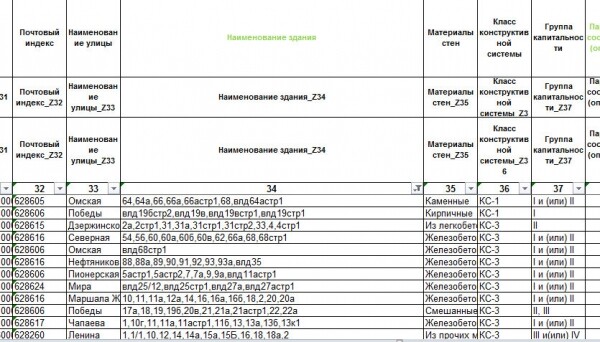
Рис.14. Пример несоответствующей записи.

Исключаем эти поля из датасета. И фиксируем изменение 214 записей.

Общее время, потраченное на этап 4 (для формулы Шумана) t4 = 2,5 час.
Количество найденных ошибок на этапе 4 (для формулы Шумана) n4 = 222 шт.

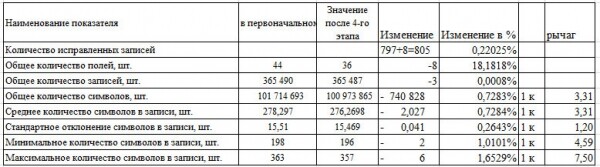
Таблица 6. Анализ показателей датасета после проведения 4-го этапа

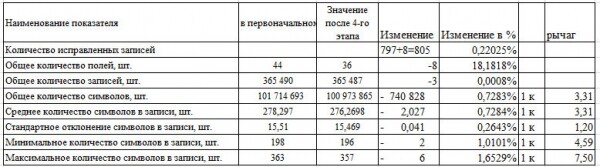
В целом анализируя изменения показателей (таблица 6) можно сказать, что:
1) Соотношение рычагов среднего количества символов к рычагу стандартного отклонения близко к 3, то есть присутствуют признаки нормального распределения (правило шести сигм).
2) Существенное отклонение рычагов минимума и максимума от рычага среднего предполагает, что исследование хвостов является перспективным направлением при поиске ошибок.

Исследуем результаты нахождения ошибок по методологии Шумана.

Холостые этапы

2.1. Общее время, потраченное на этап 2.1 (для формулы Шумана) t21 = 1 час.
Количество найденных ошибок на этапе 2.1 (для формулы Шумана) n21 = 0 шт.

3. Общее время, потраченное на этап 3 (для формулы Шумана) t3 = 0,75 час.
Количество найденных ошибок на этапе 3 (для формулы Шумана) n3 = 0 шт.

Результативные этапы
2.2. Общее время, потраченное на этап 2.2.1 (для формулы Шумана) t221 = 8 час.
Количество исправленных ошибок на этапе 2.2.1 (для формулы Шумана) n221 = 0 шт.
Общее время, потраченное на этапе 2.2.2 t222 = 4 часа.
Количество найденных ошибок на этапе 2.2.2 (для формулы Шумана) n222 = 583 шт.

Общее время, потраченное на этапе 2.2 t22 = 8 + 4 = 12 часа.
Количество найденных ошибок на этапе 2.2.2 (для формулы Шумана) n222 = 583 шт.

4. Общее время, потраченное на этап 4 (для формулы Шумана) t4 = 2,5 час.
Количество найденных ошибок на этапе 4 (для формулы Шумана) n4 = 222 шт.

Так как имеются нулевые этапы которые должны быть включены в первый этап модели Шумана, а с другой стороны этап 2.2 и 4 по своей сути независимы, то учитывая, что модель Шумана предполагает, что ростом длительности проверки, вероятность обнаружения ошибки снижается, то есть снижается поток отказов, то исследуя этот поток определим какой из этапов ставить первым, по правилу, где плотность отказа чаще, тот из этапов и ставим первым.

Рис.15.

Из формулы на рисунке 15 следует, что предпочтительней ставить четвертый этап перед этапом 2.2 в расчетах.

По формуле Шумана определяем предположительное первоначальное количество ошибок:

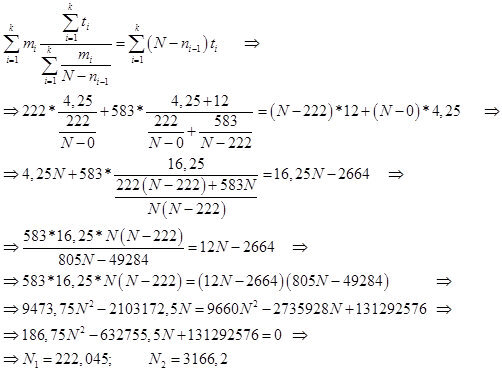
Рис.16.

Из результатов на рисунке 16 видно, что прогнозируемое количество ошибок N2 = 3167, что больше чем минимальный критерий 1459.

Мы в результате проведенного исправления исправили 805 ошибок, и прогнозируемое количество составляет 3167 – 805 = 2362, что все равно больше минимального порога принятого нами.

Определяем параметр С, лямбду и функцию надежности:

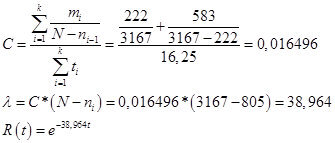
Рис.17.

По сути, лямбда — это фактический показатель с какой интенсивностью на каждом этапе обнаруживаются ошибки. Если посмотреть выше, то оценка этого показателя ранее, составляла 42,4 ошибки в час, что, достаточно, сравнимо с показателем Шумана. Обращаясь к первой части данного материала, было определено, что интенсивность нахождения ошибок разработчиком должна быть не ниже чем 1 ошибка на 250,4 записей, при проверке 1 записи в минуту. Отсюда критическое значение лямбда для модели Шумана:
60/250,4 = 0,239617.

То есть необходимость проведения процедур нахождения ошибок нужно проводить до тех пор, пока лямбда, с имеющихся 38,964, не снизится до 0,239617.

Либо пока показатель N (потенциальное количество ошибок) минус n (исправленное количество ошибок) не снизится меньше принятого нами порога (в первой части) – 1459 шт.

Часть 1. Теоретическая.

Источник: habr.com