Приводим уравнение линейной регрессии в матричный вид

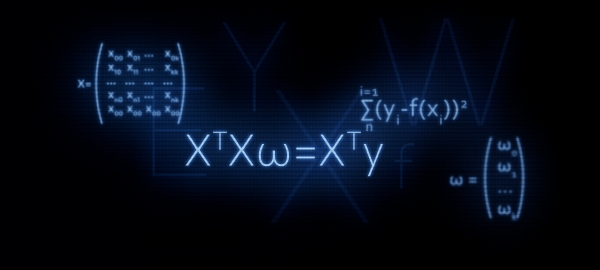
Цель статьи — оказание поддержки начинающим датасайнтистам. В предыдущей статье мы на пальцах разобрали три способа решения уравнения линейной регрессии: аналитическое решение, градиентный спуск, стохастический градиентный спуск. Тогда для аналитического решения мы применили формулу . В этой статье, как следует из заголовка, мы обоснуем применение данной формулы или другими словами, самостоятельно ее выведем.

Почему имеет смысл уделить повышенное внимание к формуле ?

Именно с матричного уравнения в большинстве случаев начинается знакомство с линейной регрессией. При этом, подробные выкладки того, как формула была выведена, встречаются редко.

Например, на курсах по машинному обучению от Яндекса, когда слушателей знакомят с регуляризацией, то предлагают воспользоваться функциями из библиотеки sklearn, при этом ни слова не упоминается о матричном представлении алгоритма. Именно в этот момент у некоторых слушателей может появится желание разобраться в этом вопросе подробнее — написать код без использования готовых функций. А для этого, надо сначала представить уравнение с регуляризатором в матричном виде. Данная статья, как раз, позволит желающим овладеть такими умениями. Приступим.

Исходные условия

Целевые показатели

У нас имеется ряд значений целевого показателя. Например, целевым показателем может быть цена на какой-либо актив: нефть, золото, пшеница, доллар и т.д. При этом, под рядом значений целевого показателя мы понимаем количество наблюдений. Такими наблюдениями могут быть, например, ежемесячные цены на нефть за год, то есть у нас будет 12 значений целевого показателя. Начнем вводить обозначения. Обозначим каждое значение целевого показателя как . Всего мы имеем наблюдений, а значит можно представить наши наблюдения как .

Регрессоры

Будем считать, что существуют факторы, которые в определенной степени объясняют значения целевого показателя. Например, на курс пары доллар/рубль сильное влияние оказывает цена на нефть, ставка ФРС и др. Такие факторы называются регрессорами. При этом, каждому значению целевого показателя должно соответствовать значение регрессора, то есть, если у нас имеется 12 целевых показателей за каждый месяц в 2018 году, то и значений регрессоров у нас тоже должно быть 12 за тот же период. Обозначим значения каждого регрессора через . Пусть в нашем случае имеется регрессоров (т.е. факторов, которые оказывают влияние на значения целевого показателя). Значит наши регрессоры можно представить следующим образом: для 1-го регрессора (например, цена на нефть): , для 2-го регрессора (например, ставка ФРС): , для «-го» регрессора:

Зависимость целевых показателей от регрессоров

Предположим, что зависимость целевого показателя от регрессоров «-го» наблюдения может быть выражена через уравнение линейной регрессии вида:

, где — «-ое» значение регрессора от 1 до ,

— количество регрессоров от 1 до

— угловые коэффициенты, которые представляют величину, на которую изменится расчетный целевой показатель в среднем при изменении регрессора.

Другими словами, мы для каждого (за исключением ) регрессора определяем «свой» коэффициент , затем перемножаем коэффициенты на значения регрессоров «-го» наблюдения, в результате получаем некое приближение «-го» целевого показателя.

Следовательно, нам нужно подобрать такие коэффициенты , при которых значения нашей апроксимирующей функции будут расположены максимально близко к значениям целевых показателей.

Оценка качества апроксиммирующей функции

Будем определять оценку качества апроксимирующей функции методом наименьших квадратов. Функция оценки качества в таком случае примет следующий вид:

Нам требуется подобрать такие значения коэффициентов $w$, при которых значение будет наименьшим.

Переводим уравнение в матричный вид

Векторное представление

Для начала, чтобы облегчить себе жизнь, следует обратить внимание на уравнение линейной регрессии и заметить, что первый коэффициент не умножается ни на один регрессор. При этом, когда мы переведем данные в матричный вид, вышеобозначенное обстоятельство будет серьезно осложнять расчеты. В этой связи предлагается ввести еще один регрессор для первого коэффициента и приравнять его единице. Вернее, каждое «-ое» значение этого регрессора приравнять единице — ведь при умножении на единицу у нас с точки зрения результата вычислений ничего не изменится, а с точки зрения правил произведения матриц, существенно сократятся наши мучения.

Теперь, на некоторое время, с целью упрощения материала, предположим, что у нас только одно «-ое» наблюдение. Тогда, представим значения регрессоров «-ого» наблюдения в качестве вектора . Вектор имеет размерность , то есть строк и 1 столбец:

Искомые коэффициенты представим в виде вектора , имеющего размерность :

Уравнение линейной регрессии для «-го» наблюдения примет вид:

Функция оценки качества линейной модели примет вид:

Обратим внимание, что в соответствии с правилами умножения матриц, нам потребовалось транспонировать вектор .

Матричное представление

В результате умножения векторов, мы получим число: , что и следовало ожидать. Это число и есть приближение «-го» целевого показателя. Но нам-то нужно приближение не одного значения целевого показателя, а всех. Для этого запишем все «-ые» регрессоры в формате матрицы . Полученная матрица имеет размерность :

Теперь уравнение линейной регрессии примет вид:

Обозначим значения целевых показателей (все ) за вектор размерностью :

Теперь мы можем записать в матричном формате уравнение оценки качества линейной модели:

Собственно, из этой формулы далее получают известную нам формулу

Как это делается? Раскрываются скобки, проводится дифференцирование, преобразуются полученные выражения и т.д., и именно этим мы сейчас и займемся.

Матричные преобразования

Раскроем скобки

Подготовим уравнение для дифференцирования

Для этого проведем некоторые преобразования. В последующих расчетах нам будет удобнее, если вектор будет представлен в начале каждого произведения в уравнении.

Преобразование 1

Как это получилось? Для ответа на этот вопрос достаточно посмотреть на размеры умножаемых матриц и увидеть, что на выходе мы получаем число или иначе .

Запишем размеры матричных выражений.

Преобразование 2

Распишем аналогично преобразованию 1

На выходе получаем уравнение, которое нам предстоит продифференцировать:

Дифференцируем функцию оценки качества модели

Продифференцируем по вектору :

Вопросов почему быть не должно, а вот операции по определению производных в двух других выражениях мы разберем подробнее.

Дифференцирование 1

Раскроем дифференцирование:

Для того, чтобы определить производную от матрицы или вектора требуется посмотреть, что у них там внутри. Смотрим:

Обозначим произведение матриц через матрицу . Матрица квадратная и более того, она симметричная. Эти свойства нам пригодятся далее, запомним их. Матрица имеет размерность :

Теперь наша задача правильно перемножить вектора на матрицу и не получить «дважды два пять», поэтому сосредоточимся и будем предельно внимательны.

Однако, замысловатое выражение у нас получилось! На самом деле мы получили число — скаляр. И теперь, уже по-настоящему, переходим к дифференцированию. Необходимо найти производную полученного выражения по каждому коэффициенту и получить на выходе вектор размерности . На всякий случай распишу процедуры по действиям:

1) продифференцируем по , получим:

2) продифференцируем по , получим:

3) продифференцируем по , получим:

На выходе — обещанный вектор размером :

Если присмотреться к вектору повнимательнее, то можно заметить, что левые и соответствующие правые элементы вектора можно сгруппировать таким образом, что в итоге из представленного вектора можно выделить вектор размера . Например, (левый элемент верхней строчки вектора) (правый элемент верхней строчки вектора) можно представить как , а — как и т.д. по каждой строчке. Сгруппируем:

Вынесем вектор и на выходе получим:

Теперь, присмотримся к получившейся матрице. Матрица представляет собой сумму двух матриц :

Вспомним, что несколько ранее, мы отметили одно важное свойство матрицы — она симметричная. Исходя из этого свойства, мы можем с уверенностью заявить, что выражение равняется . Это легко проверить, раскрыв поэлементно произведение матриц . Мы не будем делать этого здесь, желающие могут провести проверку самостоятельно.

Вернемся к нашему выражению. После наших преобразований оно получилось таким, каким мы и хотели его увидеть:

Итак, с первым дифференцированием мы справились. Переходим ко второму выражению.

Дифференцирование 2

Пойдем по протоптанной дорожке. Она будет намного короче предыдущей, так что не уходите далеко от экрана.

Раскроем поэлементно вектора и матрицу:

На время уберем из расчетов двойку — она большой роли не играет, потом вернем ее на место. Перемножим вектора на матрицу. В первую очередь умножим матрицу на вектор , здесь у нас нет никаких ограничений. Получим вектор размера :

Выполним следующее действие — умножим вектор на полученный вектор. На выходе нас будет ждать число:

Его то мы и продифференцируем. На выходе получим вектор размерности :

Что-то напоминает? Все верно! Это произведение матрицы на вектор .

Таким образом, второе дифференцирование успешно завершено.

Вместо заключения

Теперь мы знаем, как получилось равенство .

Напоследок опишем быстрый путь преобразований основных формул.

Оценим качество модели в соответствии с методом наименьших квадратов:

Дифференцируем полученное выражение:

Литература

Интернет источники:

1) habr.com/ru/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/ru/post/307004
4) nabatchikov.com/blog/view/matrix_der

Учебники, сборники задач:

1) Конспект лекций по высшей математике: полный курс / Д.Т. Письменный – 4-е изд. – М.: Айрис-пресс, 2006
2) Прикладной регрессионный анализ / Н. Дрейпер, Г. Смит – 2-е изд. – М.: Финансы и статистика, 1986 (перевод с английского)
3) Задачи на решение матричных уравнений:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html

Источник: habr.com