Привет, Хабр!
В сети Bitcoin все узлы в ходе консенсуса соглашаются над множеством UTXO: сколько монет доступно для траты, кому именно и при каких условиях. Множество UTXO — это минимально необходимый для узла-валидатора набор данных, без которого узел не сможет удостовериться в валидности приходящих транзакций и блоков, их содержащих.
В связи с этим предпринимаются попытки всячески уменьшить хранимое представление этого множества, сжать его без потери гарантий безопасности. Чем меньше объем хранимых данных, тем ниже требования к дисковому пространству узла-валидатора, что делает запуск узла-валидатора дешёвым, позволяет наращивать сеть и увеличивать тем самым устойчивость сети.
В этой заметке мы запилим Rust-прототип недавнего предложения от соавтора , — , позволяющего уменьшить требования к дисковому пространству для узлов-валидаторов.
В чём проблема?
Одной из вечных проблем Биткоина была его масштабируемость. Идея «сам себе банк» требует от участников сети вести учёт всех доступных для использования средств. В Bitcoin доступные средства выражаются в виде множества нерастраченных выходов — UTXO-set. Хотя это и не особо интуитивное представление, оно является выгодным с точки зрения производительности реализации, по сравнению с представлением, в котором у каждого «кошелька» есть «баланс» в виде отдельной записи, а также добавляет приватности (например, обеспечивает работу ).
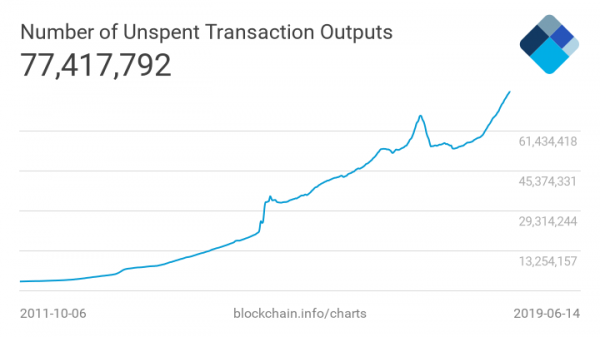
Важно различать историю транзакций (то, что зовётся блокчейном) и текущее состояние системы. История транзакций Bitcoin в настоящее время занимает порядка 200 Гб дискового пространства, и продолжает расти. Однако состояние системы гораздо меньше, порядка 4 Гб, и учитывает только факт владения монет кем-либо в настоящее время. Объем этих данных так же со-временем увеличивается, но значительно с меньшей скоростью и иногда даже имеет тенденцию к уменьшению (см. КДПВ).
Лёгкие клиенты (SPV) обменивают гарантии безопасности на возможность не хранить никакого минимального состояния (UTXO-set), кроме приватных ключей.
UTXO и UTXO-set
UTXO (Unspent Transaction Output) — нерастраченный выход транзакции, конечная точка путешествия каждого сатоши, передаваемого в транзакциях. Нерастраченные выходы становятся входами новых транзакций и при этом тратятся (spend) и удаляются из UTXO-set.
Новые UTXO всегда создаются транзакциями:
- coinbase-транзакции без входов: создают новые UTXO в ходе эмиссии монет майнерами
- обычные транзакции: создают новые UTXO, тратя при этом некий набор существующих UTXO
Процесс работы с UTXO:
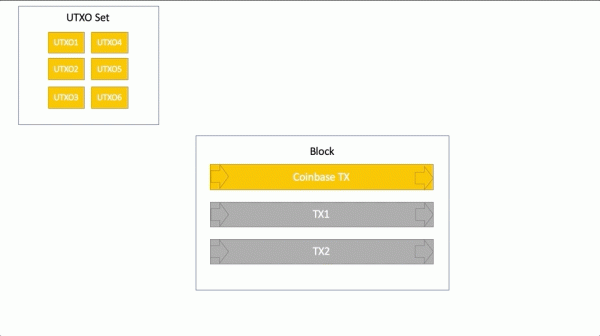
Кошельки считают количество доступных для траты монет (баланс) исходя из суммы UTXO, доступных этому кошельку для траты.
Каждый узел-валидатор, для предотвращения попыток двойной траты (double spend), должен отслеживать набор всех UTXO при проверке каждой транзакции каждого блока.
У узла должна присутствовать логика:
- Добавления в UTXO-set
- Удаления из UTXO-set
- Проверки наличия отдельно взятого UTXO в множестве
Существуют способы уменьшить требования к хранимой информации о множестве, сохранив при этом возможность добавлять и удалять элементы, проверять и доказывать существование элемента в множестве с помощью .
Аккумуляторы для UTXO
Идея применения аккумуляторов для хранения множества UTXO .
UTXO-set строится на лету, во время начальной загрузки цепочки блоков (IBD, initial block download), хранится в полном объёме и постоянно, при этом его содержимое изменяется после обработки транзакций из каждого нового и корректного блока сети. Данный процесс требует загрузки примерно 200 Гб данных блоков и проверки сотен миллионов цифровых подписей. После того, как процесс IBD закончен, в сухом остатке UTXO-set будет занимать около 4 Гб.
Однако, при использовании аккумуляторов, правила консенсуса относительно средств сводятся к проверке и генерации криптографических доказательств, а бремя отслеживания доступных средств перекладывается на плечи владельца этих средств, который предоставляет доказательства их наличия и владения ими.
Аккумулятором можно назвать компактное представление множества. Размер хранимого представления, при этом, должен быть либо постоянным  , либо увеличиваться сублинейно относительно мощности множества и размера самого элемента, например
, либо увеличиваться сублинейно относительно мощности множества и размера самого элемента, например  , где n — мощность хранимого множества.
, где n — мощность хранимого множества.
При этом аккумулятор должен позволять генерировать доказательство включения элемента в множество (inclusion proof) и давать возможность эффективно проверить это доказательство.
Аккумулятор называется динамическим если позволяет добавлять элементы и удалять элементы из множества.
Примером такого аккумулятора может послужить . Такой аккумулятор имеет постоянный размер хранимого представления, но требует наличия общего секрета (trusted setup). Это требование сводит на нет применимость такого аккумулятора для trustless-сетей типа Bitcoin, поскольку утечка данных при генерации секрета может позволить злоумышленникам создавать фальшивые доказательства существования UTXO, обманывая узлы с UTXO-set на базе такого аккумулятора.
Utreexo
Предложенная Thaddeus Dryja конструкция Utreexo позволяет создать динамический аккумулятор без trusted-setup.
Utreexo представляет собою лес из идеальных двоичных и является развитием идей, представленных в , добавляя возможность удалять элементы из множества.
Логическая структура аккумулятора
Элементы аккумулятора расположены в виде леса идеальных двоичных деревьев. Деревья упорядочены по высоте. Данное представление выбрано как наиболее наглядное и позволяет визуализировать слияние деревьев в ходе проведения операций над аккумулятором.
Автор замечает, что поскольку все деревья леса идеальны, их высота выражается степенью двойки, равно как и любое натуральное число можно представить в виде суммы степеней двойки. Соответственно, любой набор листов может быть сгруппирован в виде двоичных деревьев, а во всех случаях, добавление нового элемента требует знания лишь о корневых узлах хранимых деревьев.
Таким образом, хранимое представление аккумулятора Utreexo — это список корневых узлов (Merkle root), а не весь лес деревьев целиком.
Представим список корневых элементов как Vec<Option<Hash>>. Опциональный тип Option<Hash> говорит о том, что корневой элемент может отсутствовать, что означает, что в аккумуляторе нет дерева с соответствующей высотой.
/// SHA-256 хеш
#[derive(Copy, Clone, Hash, Eq, PartialEq)]
pub struct Hash(pub [u8; 32]);
#[derive(Debug, Clone)]
pub struct Utreexo {
pub roots: Vec<Option<Hash>>,
}
impl Utreexo {
pub fn new(capacity: usize) -> Self {
Utreexo {
roots: vec![None; capacity],
}
}
}Добавление элементов
Для начала опишем функцию parent(), которая узнаёт узел-родитель для двух заданных элементов.
Функция parent()
Поскольку мы используем деревья Меркла, то родителем каждого из двух узлов является один узел, хранящий хеш конкатенации хешей узлов-потомков:
fn hash(bytes: &[u8]) -> Hash {
let mut sha = Sha256::new();
sha.input(bytes);
let res = sha.result();
let mut res_bytes = [0u8; 32];
res_bytes.copy_from_slice(res.as_slice());
Hash(res_bytes)
}
fn parent(left: &Hash, right: &Hash) -> Hash {
let concat = left
.0
.into_iter()
.chain(right.0.into_iter())
.map(|b| *b)
.collect::<Vec<_>>();
hash(&concat[..])
}Автор замечает, что для предотвращения атак, описанных Charles Bouillaguet, Pierre-Alain Fouque, Adi Shamir, и Sebastien Zimmer в
, помимо двух хешей следует добавлять к конкатенации ещё и высоту внутри дерева.
В ходе добавления элементов в аккумулятор, необходимо отслеживать, какие корневые элементы оказываются изменены. Следуя по пути изменения корневых элементов для каждого добавляемого элемента, позднее можно сконструировать доказательство наличия этих элементов.
Отслеживание изменений в ходе добавления
Для отслеживания произведённых изменений, объявим структуру Update, которая будет хранить данные об изменениях узлов.
#[derive(Debug)]
pub struct Update<'a> {
pub utreexo: &'a mut Utreexo,
// ProofStep хранит "соседа" элемента и его положение
pub updated: HashMap<Hash, ProofStep>,
}Для добавления элемента в аккумулятор, нужно:
- Создать массив корзин корневых элементов
new_rootsи поместить туда существующие корневые элементы, по одному на каждую корзину:
Код
let mut new_roots = Vec::new();
for root in self.roots.iter() {
let mut vec = Vec::<Hash>::new();
if let Some(hash) = root {
vec.push(*hash);
}
new_roots.push(vec);
}- Дописать добавляемые элементы (массив
insertions) в первую корзинуnew_roots[0]:

Код
new_roots[0].extend_from_slice(insertions);- Провести «объединение» (coalescing) добавленных в первую корзину элементов с остальными:
- Для всех корзин, в которых больше одного элемента:
- Берём два элемента с конца корзины, вычисляем их родителя, удаляем оба элемента
- Добавляем вычисленного родителя в следующую корзину
- Для всех корзин, в которых больше одного элемента:

Код
for i in 0..new_roots.len() {
while new_roots[i].len() > 1 {
// Объединяем два элемента в один и удаляем их
let a = new_roots[i][new_roots[i].len() - 2];
let b = new_roots[i][new_roots[i].len() - 1];
new_roots[i].pop();
new_roots[i].pop();
let hash = self.parent(&a, &b);
// Наращиваем количество корзин если требуется
if new_roots.len() <= i + 1 {
new_roots.push(vec![]);
}
// Помещаем элемент в следующую корзину
new_roots[i + 1].push(hash);
// Не забываем отслеживать изменения;
// это пригодится для генерации доказательства добавления элементов
updated.insert(a, ProofStep { hash: b, is_left: false });
updated.insert(b, ProofStep {hash: a, is_left: true });
}
}- Переместить корневые элементы из корзин в результирующий массив аккумулятора
Код
for (i, bucket) in new_roots.into_iter().enumerate() {
// Наращиваем аккумулятор если требуется
if self.roots.len() <= i {
self.roots.push(None);
}
if bucket.is_empty() {
self.roots[i] = None;
} else {
self.roots[i] = Some(bucket[0]);
}
}Создание доказательства для добавленных элементов
Доказательством включения элемента в аккумулятор (Proof) будет служить путь Меркла (Merkle Path), состоящий из цепочки ProofStep. Если путь никуда не приводит, значит доказательство неверно.
/// Единичный шаг на пути к элементу в дереве Меркла.
#[derive(Debug, Copy, Clone)]
pub struct ProofStep {
pub hash: Hash,
pub is_left: bool,
}
/// Доказательство включения элемента. Содержит сам элемент и путь к нему.
#[derive(Debug, Clone)]
pub struct Proof {
pub steps: Vec<ProofStep>,
pub leaf: Hash,
}Используя полученную ранее в ходе добавления элемента информацию (структуру Update), можно создать доказательство того, что элемент был добавлен в аккумулятор. Для этого обходим таблицу сделанных изменений и добавляем каждый шаг в путь Меркла, который впоследствии и послужит доказательством:
Код
impl<'a> Update<'a> {
pub fn prove(&self, leaf: &Hash) -> Proof {
let mut proof = Proof {
steps: vec![],
leaf: *leaf,
};
let mut item = *leaf;
while let Some(s) = self.updated.get(&item) {
proof.steps.push(*s);
item = parent(&item, &s);
}
proof
}
}Процесс создания доказательства
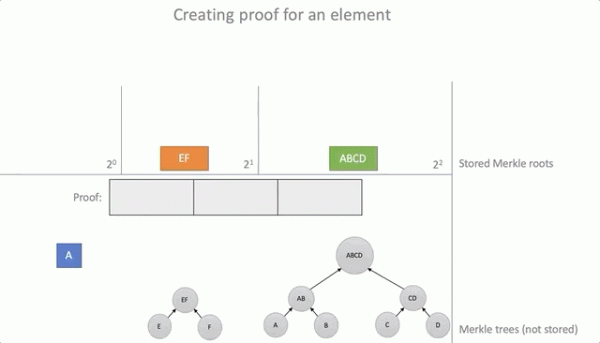
Проверка доказательства для элемента
Проверка доказательства включения элемента (inclusion proof) сводится к следованию по пути Меркла, пока он не приведёт к существующему корневому элементу:
pub fn verify(&self, proof: &Proof) -> bool {
let n = proof.steps.len();
if n >= self.roots.len() {
return false;
}
let expected = self.roots[n];
if let Some(expected) = expected {
let mut current_parent = proof.leaf;
for s in proof.steps.iter() {
current_parent = if s.is_left {
parent(&s.hash, ¤t_parent)
} else {
parent(¤t_parent, &s.hash)
};
}
current_parent == expected
} else {
false
}
}Наглядно:
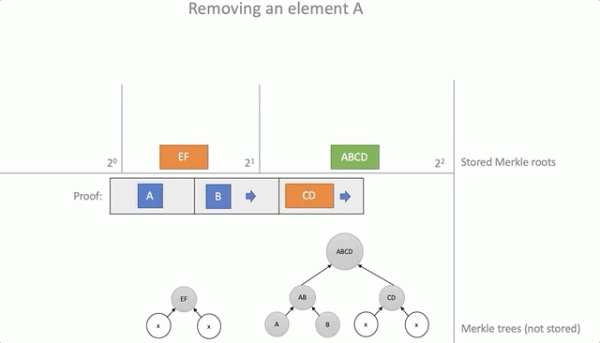
Процесс проверки доказательства для A
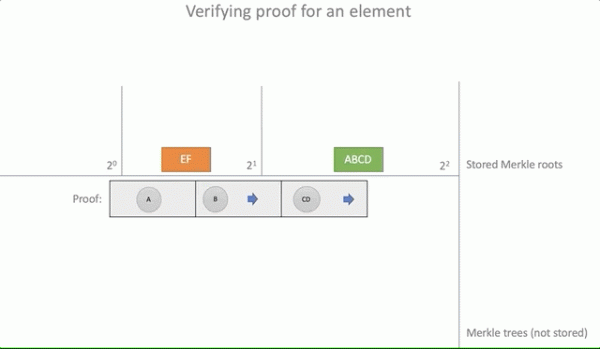
Удаление элементов
Для удаления элемента из аккумулятора требуется предоставить валидное доказательство того, что элемент там находится. Используя данные из доказательства, можно вычислить новые корневые элементы аккумулятора, для которых данное доказательство больше не будет верным.
Алгоритм следующий:
- Как и при добавлении, организуем набор пустых корзин, соответствующих деревьям Меркла с высотой равной степени двойки от индекса корзины
- Вставляем в корзины элементы из шагов пути Меркла; индекс корзины равен номеру текущего шага
- Удаляем корневой элемент, к которому приводит путь из доказательства
- Как и при добавлении, вычисляем новые корневые элементы, обьединяя попарно элементы из корзин и перемещая результат объединения в следующую корзину
Код
fn delete(&self, proof: &Proof, new_roots: &mut Vec<Vec<Hash>>) -> Result<(), ()> {
if self.roots.len() < proof.steps.len() || self.roots.get(proof.steps.len()).is_none() {
return Err(());
}
let mut height = 0;
let mut hash = proof.leaf;
let mut s;
loop {
if height < new_roots.len() {
let (index, ok) = self.find_root(&hash, &new_roots[height]);
if ok {
// Remove hash from new_roots
new_roots[height].remove(index);
loop {
if height >= proof.steps.len() {
if !self.roots[height]
.and_then(|h| Some(h == hash))
.unwrap_or(false)
{
return Err(());
}
return Ok(());
}
s = proof.steps[height];
hash = self.parent(&hash, &s);
height += 1;
}
}
}
if height >= proof.steps.len() {
return Err(());
}
while height > new_roots.len() {
new_roots.push(vec![]);
}
s = proof.steps[height];
new_roots[height].push(s.hash);
hash = self.parent(&hash, &s);
height += 1;
}
}Процесс удаления элемента «А»:
Интеграция в существующую сеть
Используя предложенный аккумулятор, узлы могут отказаться от использования БД для хранения всех UTXO, сохраняя при этом возможность изменять UTXO-set. Однако возникает проблема работы с доказательствами.
Назовём узел-валидатор, который использует аккумулятор UTXO компактным (compact-state node), а валидатор без аккумулятора — полным (full node). Существование двух классов узлов создаёт проблему интеграции их в единую сеть, поскольку компактные узлы требуют доказательства существования UTXO, которые тратятся в транзакциях, а полные узлы — нет. Если все узлы сети одновременно и скоординировано не перейдут на использование Utreexo, тогда компактные узлы останутся позади и не смогут работать в сети Bitcoin.
Для решения проблемы интеграции компактных узлов в сеть, предлагается ввести дополнительный класс узлов — мосты. Узел-мост — это полный узел, который ко всему прочему хранит аккумулятор Utreexo и доказательства включения для всех UTXO из UTXO-set. Мосты вычисляют новые хеши и обновляют аккумулятор и доказательства по мере поступления новых блоков с транзакциями. Поддержка и обновление аккумулятора и доказательств не накладывает дополнительной вычислительной нагрузки на такие узлы. Мосты жертвуют дисковым пространством: требуется хранить порядка  хешей, по сравнению с
хешей, по сравнению с  хешей для компактных узлов, где n — мощность множества UTXO.
хешей для компактных узлов, где n — мощность множества UTXO.
Архитектура сети
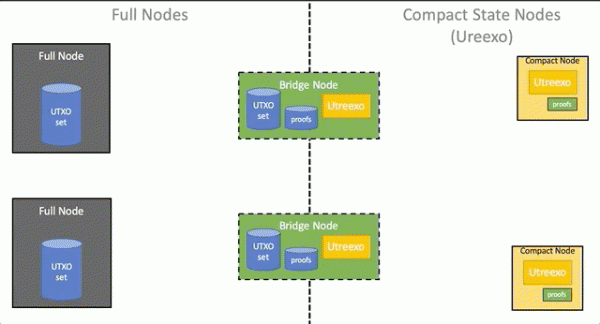
Мосты дают возможность постепенно добавлять компактные узлы в сеть без изменения ПО существующих узлов. Полные узлы работают как и раньше, распространяя транзакции и блоки между собой. Узлы-мосты представляют собою полные узлы, которые дополнительно хранят данные аккумулятора Utreexo и набор доказательств включения для всех UTXO на данный момент. Мостовой узел никак не афиширует себя как таковой, прикидываясь полным узлом для всех полных узлов и компактным узлом — для всех компактных. Хотя мосты и соединяют обе сети вместе, в действительности требуется соединять их только в одном направлении: от существующих полных узлов к компактным узлам. Это возможно из-за того, что формат транзакций не требуется изменять, а доказательства для UTXO для компактных узлов может быть отброшено, поэтому любой компактный узел точно так же может рассылать транзакции всем участникам сети без участия узлов-мостов.
Заключение
Мы рассмотрели аккумулятор Utreexo и реализовали его прототип на языке Rust. Рассмотрели архитектуру сети, которая позволит интегрировать узлы на базе аккумулятора. Преимуществом компактных улов выступает размер хранимых данных, который зависит логарифмически от мощности множества UTXO, что сильно снижает требования к дисковому пространству и производительности хранилища для таких узлов. Недостатком выступает дополнительный трафик узлов на передачу доказательств, но техники агрегации доказательств (когда одно доказательство доказывает существование нескольких элементов) и кеширования могут помочь удержать трафик в приемлемых пределах.
Ссылки:
- —
Источник: habr.com


