
Статья от команды Stitch Fix предлагает использовать подход клинических исследований не меньшей эффективности (non-inferiority trials) в маркетинговых и продуктовых A/B тестах. Такой подход действительно применим, когда мы тестируем новое решение, имеющее преимущества, неизмеряемые тестами.
Самый простой пример — снижение костов. Например, автоматизируем процесс назначения первого урока, но не хотим сильно уронить сквозную конверсию. Или тестируем изменения, которые ориентированы на один сегмент пользователей, при этом следим, чтобы конверсии по другим сегментам просели не сильно (при тестировании нескольких гипотез не забываем про поправки).
Выбор правильной границы не меньшей эффективности добавляет дополнительные трудности на этапе дизайна теста. Вопрос, как выбирать Δ в статье не очень хорошо раскрыт. Кажется, что этот выбор не до конца прозрачен и в клинических испытаниях. медицинских публикаций по non-inferiority сообщает, что только в половине публикаций выбор границы обосновывается и часто эти обоснования неоднозначны или не подробны.
В любом случае, этот подход кажется интересным, т.к. за счет уменьшения необходимого размера выборки может увеличить скорость тестирования, а, значит, и скорость принятия решений. — Дарья Мухина, продуктовый аналитик мобильного приложения Skyeng.
Команда Stitch Fix любит тестировать разные вещи. Все технологическое сообщество в принципе любит проводить тесты. Какая версия сайта привлекает больше пользователей – A или B? Приносит ли версия А рекомендательной модели больше денег, чем версия B? Почти всегда для проверки гипотез мы используем самый простой подход из базового курса статистики:
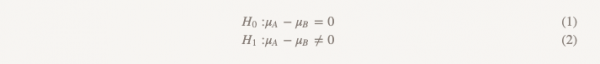
Хотя мы редко используем этот термин, такая форма тестирования называется «проверка гипотезы о превосходстве ». При таком подходе мы предполагаем, что между двумя вариантами нет никакой разницы. Мы придерживаемся этой идеи и отказываемся от нее только в том случае, если полученные данные оказываются достаточно убедительными для этого – то есть демонстрируют, что один из вариантов (A или B) лучше, чем другой.
Проверка гипотезы о превосходстве подходит для решения множества проблем. Мы выпускаем В-версию рекомендательной модели только в том случае, если она очевидно лучше уже используемой версии A. Но в некоторых случаях этот подход работает не так хорошо. Рассмотрим несколько примеров.
1) Мы используем сторонний сервис, который помогает идентифицировать поддельные банковские карты. Мы нашли другой сервис, который стоит значительно меньше. Если более дешевый сервис работает настолько же хорошо, как и тот, что мы используем сейчас, мы выберем его. Он не обязательно должен быть лучше используемого сервиса.
2) Мы хотим отказаться от источника данных A и заменить его на источник данных B. Мы могли бы отложить отказ от A, если B выдает очень плохие результаты, но продолжать использовать A не представляется возможным.
3) Мы хотели бы перейти от подхода к моделированиюA к подходу B не потому, что мы ожидаем лучших результатов от B, а потому, что это дает нам большую оперативную гибкость. У нас нет оснований полагать, что В будет хуже, но мы не станем осуществлять переход, если это будет так.
4) Мы внесли несколько качественных изменений в дизайн веб-сайта (версия В) и считаем, что эта версия превосходит версию А. Мы не ожидаем изменений в конверсии или каких-либо ключевых показателях эффективности, по которым мы обычно оцениваем веб-сайт. Но мы считаем, что есть преимущества в параметрах, которые либо неизмеримы, либо наших технологий недостаточно для измерения.
Во всех этих случаях исследование превосходства — не самое подходящее решение. Но большинство специалистов в таких ситуациях используют его по умолчанию. Мы тщательно проводим эксперимент, чтобы правильно определить величину эффекта. Если бы было верно, что версии A и B работают очень схожим образом, есть вероятность, что нам не удастся отклонить нулевую гипотезу. Делаем ли мы вывод, что А и В в целом работают одинаково? Нет! Невозможность отклонить нулевую гипотезу и принятие нулевой гипотезы — не одно и то же.
Расчеты объема выборки (которые вы, конечно же, проводили), как правило, проводятся с более строгими границами для ошибки первого рода (вероятность ошибочного отклонения нулевой гипотезы, часто называемая альфа), чем для ошибки второго рода (вероятность неспособности отклонить нулевую гипотезу, при условии, что нулевая гипотеза ошибочна, часто называемая бета). Типичное значение для альфа составляет 0,05, тогда как типичное значение для бета составляет 0,20, что соответствует статистической мощности 0,80. Это означает, что с мы можем не обнаружить истинное влияние величины, которую мы указали в наших расчетах мощности, с вероятностью 20% и это довольно серьезный пробел в информации. В качестве примера давайте рассмотрим такие гипотезы:

H0: мой рюкзак НЕ в моей комнате (3)
H1: мой рюкзак в моей комнате (4)
Если я обыскал свою комнату и нашел свой рюкзак — отлично, я могу отказаться от нулевой гипотезы. Но если я осмотрел комнату и не смог найти свой рюкзак (рисунок 1), какой вывод я должен сделать? Уверен ли я, что его там нет? Достаточно ли тщательно я искал? Что если я обыскал только 80% комнаты? Сделать вывод, что рюкзака точно нет в комнате, будет опрометчивым решением. Неудивительно, что мы не можем «принять нулевую гипотезу».

Область, которую мы обыскали
Мы не нашли рюкзак — должны ли мы принять нулевую гипотезу?
Рисунок 1. Обыскать 80% комнаты — это примерно то же самое, что провести исследование с мощностью 80%. Если вы не нашли рюкзак, осмотрев 80% комнаты, можно ли сделать вывод, что его там нет?
Так что же делать специалисту по данным в этой ситуации? Вы можете сильно увеличить мощность исследования, но тогда вам понадобится выборка намного большего размера, а результат все равно будет неудовлетворительным.
К счастью, подобные проблемы давно изучаются в мире клинических исследований. Препарат B дешевле, чем препарат A; ожидается, что препарат B будет вызывать меньше побочных эффектов, чем препарат А; препарат B легче транспортировать, потому что его не нужно хранить в холодильнике, а препарат A – нужно. Проверим гипотезу о не меньшей эффективности. Это нужно, чтобы показать, что версия B так же хороша, как и версия A — по крайней мере, в пределах некоторого заранее определенного предела “не меньшей эффективности”, Δ. Чуть позже мы подробнее поговорим о том, как установить этот предел. Но сейчас предположим, что это минимальная разница, которая практически значима (в контексте клинических испытаний это обычно называется клинической значимостью).
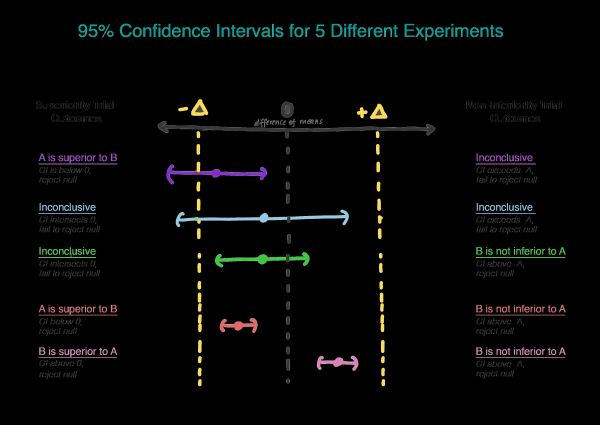
Гипотезы о не меньшей эффективности переворачивают все с ног на голову:
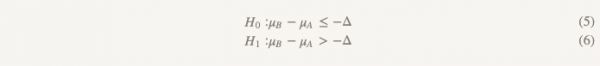
Теперь вместо того, чтобы предполагать, что разницы нет, мы предполагаем, что версия B хуже, чем версия A, и мы будем придерживаться этого предположения, пока не продемонстрируем, что это не так. Это как раз тот момент, когда имеет смысл использовать тестирование односторонней гипотезы! На практике это можно сделать, построив доверительный интервал и определив, действительно ли интервал больше, чем Δ (рисунок 2).
Выбор Δ
Как правильно выбрать Δ? Процесс выбора Δ включает статистическое обоснование и предметную оценку. В мире клинических исследований существуют нормативные рекомендации, из которых следует, что дельта должна представлять собой наименьшее клинически значимое различие — такое, которое будет иметь значение на практике. Вот цитата из европейского руководства, с помощью которой можно себя проверить: «Если разница была выбрана правильно, доверительный интервал, который полностью лежит между –∆ и 0…, все еще достаточен для демонстрации не меньшей эффективности. Если этот результат не кажется приемлемым, это означает, что ∆ не был выбран надлежащим образом».
Дельта определенно не должна превышать величину эффекта версии A по отношению к истинному контролю (плацебо / отсутствие лечения), поскольку это приводит нас к тому, то версия B хуже, чем истинный контроль, и в то же время демонстрирует «не меньшую эффективность». Предположим, что когда была представлена версия A, на ее месте была версия 0 или функция вообще не существовала (см. рисунок 3).
По результатам проверки гипотезы о превосходстве была выявлена величина эффекта E (то есть предположительно μ^A−μ^0=E). Теперь А — наш новый стандарт, и мы хотим убедиться, что В не уступает А. Еще один способ записать μB−μA≤−Δ (нулевая гипотеза) — μB≤μA−Δ. Если мы допустим, что делать равна или превышает E, то μB ≤ μA−E ≤ плацебо. Теперь мы видим, что наша оценка для μB полностью превышает μA−E, что тем самым полностью опровергает нулевую гипотезу и позволяет сделать вывод, что В не уступает А, но в то же время μB может быть ≤ μ плацебо, а это не то, что нам нужно. (рисунок 3).
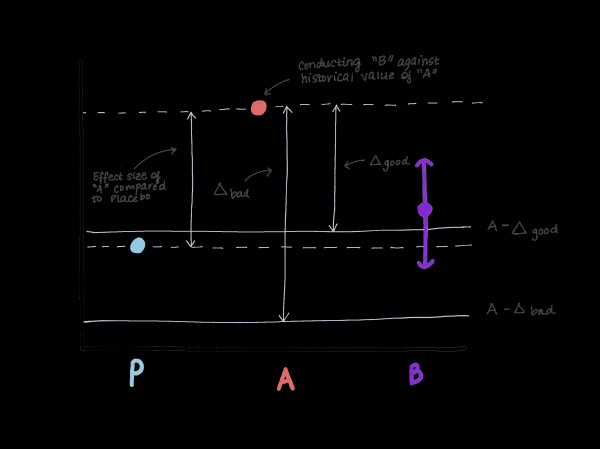
Рисунок 3. Демонстрация рисков выбора границы не меньшей эффективности. Если предел слишком велик, можно сделать вывод, что B не уступает A, но в то же время неотличим от плацебо. Мы не станем менять препарат, который явно эффективнее плацебо (А), на препарат, который имеет такую же эффективность, что и плацебо.
Выбор α
Перейдем к выбору α. Можно использовать стандартное значение α = 0,05, но это не совсем честно. Как, например, когда вы покупаете что-то в интернете и используете сразу несколько кодов на скидку, хотя они не должны суммироваться — просто разработчик допустил ошибку, а вам это сошло с рук. По правилам значение α должно быть быть равно половине значения α, которое используется при проверке гипотезы о превосходстве, то есть 0,05 / 2 = 0,025.
Размер выборки
Как оценить размер выборки? Если вы считаете, что истинное разницы средних между A и B равно 0, тогда расчет размера выборки будет таким же, как и при проверке гипотезы о превосходстве, за исключением того, что вы заменяете размер эффекта пределом не меньшей эффективности, при условии, что вы используете αне меньшая эффективность = 1/2αпревосходство (αnon-inferiority=1/2αsuperiority). Если у вас есть основания полагать, что вариант B может быть немного хуже, чем вариант A, но вы хотите доказать, что он хуже не более чем на Δ, тогда вам повезло! Фактически это уменьшает размер вашей выборки, потому что легче продемонстрировать, что B хуже, чем A, если вы на самом деле считаете, что он немного хуже, а не равноценен.
Пример с решением
Предположим, вы хотите перейти на версию В при условии, что она хуже версии А не более чем на 0,1 пункта по 5-бальной шкале удовлетворенности клиентов… Подойдем к этой задаче, используя гипотезу о превосходстве.
Для проверки гипотезы о превосходстве мы бы рассчитывали размер выборки следующим образом:

То есть если у вас в группе будет 2103 наблюдения, вы можете быть на 90 % уверены, что обнаружите эффект величиной 0,10 или больше. Но если значение 0,10 для вас слишком велико, возможно, не стоит для него проверять гипотезу о превосходстве. Возможно, для надежности вы решите провести исследование для меньшего размера эффекта, например 0,05. В этом случае вам потребуется 8407 наблюдений, то есть выборка увеличится почти в 4 раза. Но что если мы будем придерживаться нашего исходного размера выборки, но увеличим мощность до 0,99, чтобы мы не сомневались, если получим положительный результат? В таком случае n для одной группы составит 3676, что уже лучше, но увеличивает размер выборки более чем на 50 %. И в результате мы все равно просто не сможем опровергнуть нулевую гипотезу, а не получим ответ на свой вопрос.
Что если вместо этого мы проверим гипотезу о не меньшей эффективности?
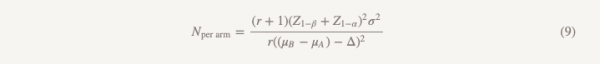
Размер выборки будет рассчитывать по такой же формуле за исключением знаменателя.
Отличия от формулы, используемой при проверки гипотезы о превосходстве, заключаются в следующем:
— Z1−α/2 заменяется на Z1−α, но если вы делаете все по правилам, вы заменяете α = 0,05 на α = 0,025, то есть, это одно и то же число (1,96)
— в знаменателе появляется (μB−μA)
— θ(величина эффекта) заменяется Δ (предел не меньшей эффективности)
Если мы предположим, что µB = µA, то (µB − µA) = 0 и расчет размера выборки для предела не меньшей эффективности это именно то, что мы получили бы при вычислении превосходства для величины эффекта 0,1, отлично! Мы можем провести исследование одного и того же масштаба с разными гипотезами и другим подходом к выводам, и мы получим ответ на вопрос, на который мы действительно хотим ответить.
Теперь предположим, что мы на самом деле не считаем, что µB = µA и
думаем, что µB немного хуже, может быть, на 0,01 единицы. Это увеличивает наш знаменатель, уменьшая размер выборки на группу до 1737.
Что произойдет, если версия B на самом деле лучше, чем версия A? Мы опровергаем нулевую гипотезу о том, что B хуже, чем A, более чем на Δ и примем альтернативную гипотезу о том, что B, если хуже, не хуже чем на Δ, и может быть лучше. Попробуйте занести это заключение в кросс-функциональную презентацию и посмотрите, что из этого получится (серьезно, попробуйте). В ситуации, когда нужно ориентироваться на перспективу, никто не хочет соглашаться на «хуже не более чем на Δ и, возможно, лучше».
В этом случае мы можем провести исследование, которое называется очень кратко «проверка гипотезы о том, что один из вариантов превосходит другой или уступает ему». В нем используются два набора гипотез:
Первый набор (такой же, как при проверке гипотезы о не меньшей эффективности):
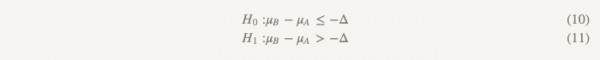
Второй набор (такой же, как при проверке гипотезы о превосходстве):
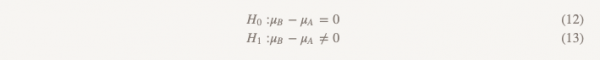
Мы проверяем вторую гипотезу только в том случае, если отклонена первая. При последовательном тестировании мы сохраняем общий уровень ошибок первого рода (α). На практике это может быть достигнуто путем создания 95 % доверительного интервала для разницы между средними и проверки, чтобы определить, превышает ли весь интервал -Δ. Если интервал не превышает -Δ, мы не можем отклонить нулевое значение и остановиться. Если весь интервал действительно превышает −Δ, мы продолжим и посмотрим, содержит ли интервал 0.
Существует еще один тип исследований, который мы не обсудили – исследования эквивалентности.
Исследования этого типа могут заменяться исследованиями для проверки гипотезы о не меньшей эффективности и наоборот, но на самом у них есть важное отличие. Испытание для проверки гипотезы о не меньшей эффективности нацелена на то, чтобы показать, что вариант B как минимум так же хорош, как A. А исследование эквивалентности нацелено на то, чтобы показать, что вариант B как минимум так же хорош, как A, а вариант A как так же хорош, как B, что сложнее. В сущности, мы пытаемся определить, лежит ли весь доверительный интервал для разности средних между −Δ и Δ. Такие исследования требуют большего размера выборки и проводятся реже. Поэтому в следующий раз, когда вы будете проводить исследование, в котором ваша главная задача — убедиться, что новая версия не хуже, не соглашайтесь на «неспособность опровергнуть нулевую гипотезу». Если вы хотите проверить действительно важную гипотезу., рассмотрите различные варианты.
Источник: habr.com



